Linear algebra

The @ operator

at.matmul implements the @ operator on tensors.

Matrix and vector products

dot(l, r)	Return a symbolic dot product.
batched_dot(a, b)	Compute the batched dot product of two variables.
outer(x, y)	Return vector-vector outer product.
matmul(x1, x2[, dtype])	Compute the matrix product of two tensor variables.
tensordot(a, b[, axes])	Compute a generalized dot product over provided axes.
batched_tensordot(x, y[, axes])	Compute a batched tensordot product.
nlinalg.matrix_power(M, n)	Raise a square matrix, M, to the (integer) power n.
nlinalg.matrix_dot(*args)	Shorthand for product between several dots.
slinalg.kron(a, b)	Kronecker product.

aesara.tensor.dot(X, Y)

For 2-D arrays it is equivalent to matrix multiplication, and for 1-D arrays to inner product of vectors (without complex conjugation). For N dimensions it is a sum product over the last axis of a and the second-to-last of b:

Parameters:

• X (symbolic tensor) – left term

• Y (symbolic tensor) – right term

Return type:

symbolic matrix or vector

Returns:

the inner product of X and Y.

aesara.tensor.outer(X, Y)

Parameters:

• X (symbolic vector) – left term

• Y (symbolic vector) – right term

Return type:

symbolic matrix

Returns:

vector-vector outer product

aesara.tensor.tensordot(a, b, axes=2)

Given two tensors a and b,tensordot computes a generalized dot product over the provided axes. Aesara’s implementation reduces all expressions to matrix or vector dot products and is based on code from Tijmen Tieleman’s gnumpy (http://www.cs.toronto.edu/~tijmen/gnumpy.html).

Parameters:

• a (symbolic tensor) – the first tensor variable

• b (symbolic tensor) – the second tensor variable

• axes (int or array-like of length 2) –

  an integer or array. If an integer, the number of axes to sum over. If an array, it must have two array elements containing the axes to sum over in each tensor.

  Note that the default value of 2 is not guaranteed to work for all values of a and b, and an error will be raised if that is the case. The reason for keeping the default is to maintain the same signature as NumPy’s tensordot function (and np.tensordot raises analogous errors for non-compatible inputs).

  If an integer i, it is converted to an array containing the last i dimensions of the first tensor and the first i dimensions of the second tensor:

  axes = [range(a.ndim - i, b.ndim), range(i)]

  If an array, its two elements must contain compatible axes of the two tensors. For example, [[1, 2], [2, 0]] means sum over the 2nd and 3rd axes of a and the 3rd and 1st axes of b. (Remember axes are zero-indexed!) The 2nd axis of a and the 3rd axis of b must have the same shape; the same is true for the 3rd axis of a and the 1st axis of b.

Returns:

a tensor with shape equal to the concatenation of a’s shape (less any dimensions that were summed over) and b’s shape (less any dimensions that were summed over).

Return type:

symbolic tensor

It may be helpful to consider an example to see what tensordot does. Aesara’s implementation is identical to NumPy’s. Here a has shape (2, 3, 4) and b has shape (5, 6, 4, 3). The axes to sum over are [[1, 2], [3, 2]] – note that a.shape[1] == b.shape[3] and a.shape[2] == b.shape[2]; these axes are compatible. The resulting tensor will have shape (2, 5, 6) – the dimensions that are not being summed:

import numpy as np

a = np.random.random((2,3,4))
b = np.random.random((5,6,4,3))

c = np.tensordot(a, b, [[1,2],[3,2]])

a0, a1, a2 = a.shape
b0, b1, _, _ = b.shape
cloop = np.zeros((a0,b0,b1))

# Loop over non-summed indices--these exist in the tensor product
for i in range(a0):
    for j in range(b0):
        for k in range(b1):
            # Loop over summed indices--these don't exist in the tensor product
            for l in range(a1):
                for m in range(a2):
                    cloop[i,j,k] += a[i,l,m] * b[j,k,m,l]

assert np.allclose(c, cloop)

This specific implementation avoids a loop by transposing a and b such that the summed axes of a are last and the summed axes of b are first. The resulting arrays are reshaped to 2 dimensions (or left as vectors, if appropriate) and a matrix or vector dot product is taken. The result is reshaped back to the required output dimensions.

In an extreme case, no axes may be specified. The resulting tensor will have shape equal to the concatenation of the shapes of a and b:

>>> c = np.tensordot(a, b, 0)
>>> a.shape
(2, 3, 4)
>>> b.shape
(5, 6, 4, 3)
>>> print(c.shape)
(2, 3, 4, 5, 6, 4, 3)

Note:

See the documentation of numpy.tensordot for more examples.

aesara.tensor.batched_dot(X, Y)

Parameters:

• x – A Tensor with sizes e.g.: for 3D (dim1, dim3, dim2)

• y – A Tensor with sizes e.g.: for 3D (dim1, dim2, dim4)

This function computes the dot product between the two tensors, by iterating over the first dimension using scan. Returns a tensor of size e.g. if it is 3D: (dim1, dim3, dim4) Example:

>>> first = at.tensor3('first')
>>> second = at.tensor3('second')
>>> result = batched_dot(first, second)

Note:

This is a subset of numpy.einsum, but we do not provide it for now.

Parameters:

• X (symbolic tensor) – left term

• Y (symbolic tensor) – right term

Returns:

tensor of products

aesara.tensor.batched_tensordot(X, Y, axes=2)

Parameters:

• x – A Tensor with sizes e.g.: for 3D (dim1, dim3, dim2)

• y – A Tensor with sizes e.g.: for 3D (dim1, dim2, dim4)

• axes (int or array-like of length 2) –

  an integer or array. If an integer, the number of axes to sum over. If an array, it must have two array elements containing the axes to sum over in each tensor.

  If an integer i, it is converted to an array containing the last i dimensions of the first tensor and the first i dimensions of the second tensor (excluding the first (batch) dimension):

  axes = [range(a.ndim - i, b.ndim), range(1,i+1)]
  

  If an array, its two elements must contain compatible axes of the two tensors. For example, [[1, 2], [2, 4]] means sum over the 2nd and 3rd axes of a and the 3rd and 5th axes of b. (Remember axes are zero-indexed!) The 2nd axis of a and the 3rd axis of b must have the same shape; the same is true for the 3rd axis of a and the 5th axis of b.

Returns:

a tensor with shape equal to the concatenation of a’s shape (less any dimensions that were summed over) and b’s shape (less first dimension and any dimensions that were summed over).

Return type:

tensor of tensordots

A hybrid of batch_dot and tensordot, this function computes the tensordot product between the two tensors, by iterating over the first dimension using scan to perform a sequence of tensordots.

Note:

See tensordot() and batched_dot() for supplementary documentation.

Decompositions

nlinalg.qr(a[, mode])	Computes the QR decomposition of a matrix.
nlinalg.svd(a[, full_matrices, compute_uv])	This function performs the SVD on CPU.

Matrix eigenvalues

nlinalg.eigh(a[, UPLO])
slinalg.eigvalsh(a, b[, lower])

Norms and other numbers

nlinalg.norm(x, ord)
nlinalg.trace(X)	Returns the sum of diagonal elements of matrix X.

Solving equations and inverting matrices

nlinalg.tensorsolve(a, b[, axes])	Aesara utilization of numpy.linalg.tensorsolve.
nlinalg.pinv(x[, hermitian])	Computes the pseudo-inverse of a matrix .
nlinalg.tensorinv(a[, ind])	Aesara utilization of numpy.linalg.tensorinv;
nlinalg.lstsq
nlinalg.matrix_inverse	Computes the inverse of a matrix .
slinalg.solve(a, b[, assume_a, lower, ...])	Solves the linear equation set a * x = b for the unknown x for square a matrix.
slinalg.cho_solve(c_and_lower, b[, check_finite])	Solve the linear equations A x = b, given the Cholesky factorization of A.
slinalg.solve_triangular(a, b[, trans, ...])	Solve the equation a x = b for x, assuming a is a triangular matrix.
slinalg.solve_discrete_lyapunov(A, Q[, method])	Solve the discrete Lyapunov equation .
slinalg.solve_continuous_lyapunov(A, Q)	Solve the continuous Lyapunov equation .
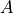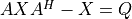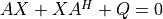