Creating a new Op: Python implementation#
So suppose you have looked through the library documentation and you don’t see a function that does what you want.
If you can implement something in terms of an existing Op, you should do that. Odds are your function that uses existing Aesara expressions is short, has no bugs, and potentially profits from rewrites that have already been implemented.
However, if you cannot implement an Op in terms of an existing Op, you have to
write a new one.
As an illustration, this tutorial will demonstrate how a simple Python-based
Op that performs operations on np.float64s is written.
Note
This is an introductury tutorial and as such it does not cover how to make
an Op that returns a view or modifies the values in its inputs. Thus, all
Ops created with the instructions described here MUST return newly
allocated memory or reuse the memory provided in the parameter
output_storage of the Op.perform() method. See
Views and inplace operations for an explanation on how to do this.
If your Op returns a view or changes the value of its inputs
without doing as prescribed in that page, Aesara will run, but will
return correct results for some graphs and wrong results for others.
It is recommended that you run your tests in DebugMode, since it
can help verify whether or not your Op behaves correctly in this
regard.
Aesara Graphs refresher#
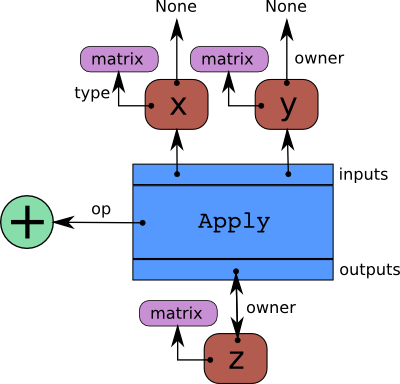
Aesara represents symbolic mathematical computations as graphs. Those graphs
are bi-partite graphs (graphs with two types of nodes), they are composed of
interconnected Apply and Variable nodes.
Variable nodes represent data in the graph, either inputs, outputs or
intermediary values. As such, inputs and outputs of a graph are lists of Aesara
Variable nodes. Apply nodes perform computation on these
variables to produce new variables. Each Apply node has a link to an
instance of Op which describes the computation to perform. This tutorial
details how to write such an Op instance. Please refers to
Graph Structures for a more detailed explanation about the graph
structure.
Op’s basic methods#
An Op is any Python object which inherits from Op.
This section provides an overview of the basic methods you typically have to
implement to make a new Op. It does not provide extensive coverage of all the
possibilities you may encounter or need. For that refer to
Ops.
import aesara
from aesara.graph.op import Op
class MyOp(Op):
# Properties attribute
__props__ = ()
#itypes and otypes attributes are
#compulsory if make_node method is not defined.
#They're the type of input and output respectively
itypes = None
otypes = None
#Compulsory if itypes and otypes are not defined
def make_node(self, *inputs):
pass
# Python implementation:
def perform(self, node, inputs_storage, output_storage):
pass
# Other type of implementation
# C implementation: [see aesara web site for other functions]
def c_code(self, node, inputs, outputs, sub):
pass
# Other implementations:
def make_thunk(self, node, storage_map, _, _2, impl=None):
pass
# optional:
check_input = True
def __init__(self, *args):
pass
def grad(self, inputs, g):
pass
def R_op(self, inputs, eval_points):
pass
def infer_shape(self, fgraph, node, input_shapes):
pass
An Op has to implement some methods defined in the the interface of
Op. More specifically, it is mandatory for an Op to define either
the method Op.make_node() or Op.itypes, Op.otypes and one of the
implementation methods, either Op.perform(), COp.c_code()
or Op.make_thunk().
Op.make_node()method creates an Apply node representing the application of theOpon the inputs provided. This method is responsible for three things:
it first checks that the input
Variables types are compatible with the currentOp. If theOpcannot be applied on the provided input types, it must raises an exception (such asTypeError).it operates on the
Variables found in*inputsin Aesara’s symbolic language to infer the type of the symbolic outputVariables. It creates outputVariables of a suitable symbolicTypeto serve as the outputs of thisOp’s application.it creates an
Applyinstance with the input and outputVariable, and return theApplyinstance.
Op.perform()method defines the Python implementation of anOp. It takes several arguments:
nodeis a reference to an Apply node which was previously obtained via theOp.make_node()method. It is typically not used in a simpleOp, but it contains symbolic information that could be required by a complexOp.
inputsis a list of references to data which can be operated on using non-symbolic statements, (i.e., statements in Python, Numpy).
output_storageis a list of storage cells where the output is to be stored. There is one storage cell for each output of theOp. The data put inoutput_storagemust match the type of the symbolic output. It is forbidden to change the length of the list(s) contained inoutput_storage. A function Mode may allowoutput_storageelements to persist between evaluations, or it may resetoutput_storagecells to hold a value ofNone. It can also pre-allocate some memory for theOpto use. This feature can allowperformto reuse memory between calls, for example. If there is something preallocated in theoutput_storage, it will be of the good dtype, but can have the wrong shape and have any stride pattern.
Op.perform()method must be determined by the inputs. That is to say, when applied to identical inputs the method must return the same outputs.An
Ops implementation can be defined in other ways, as well. For instance, it is possible to define a C-implementation viaCOp.c_code(). Please refers to tutorial Extending Aesara with a C Op for a description ofCOp.c_code()and other relatedc_**methods. Note that anOpcan provide both Python and C implementations.
Op.make_thunk()method is another alternative toOp.perform(). It returns a thunk. A thunk is defined as a zero-arguments function which encapsulates the computation to be performed by anOpon the arguments of its corresponding node. It takes several parameters:
nodeis theApplyinstance for which a thunk is requested,
storage_mapis adictof lists which maps variables to a one-element lists holding the variable’s current value. The one-element list acts as pointer to the value and allows sharing that “pointer” with other nodes and instances.
compute_mapis also a dict of lists. It maps variables to one-element lists holding booleans. If the value is 0 then the variable has not been computed and the value should not be considered valid. If the value is 1 the variable has been computed and the value is valid. If the value is 2 the variable has been garbage-collected and is no longer valid, but shouldn’t be required anymore for this call. The returned function must ensure that it sets the computed variables as computed in thecompute_map.
implallow to select between multiple implementation. It should have a default value ofNone.
Op.make_thunk()is useful if you want to generate code and compile it yourself.If
Op.make_thunk()is defined by anOp, it will be used by Aesara to obtain theOp’s implementation.Op.perform()andCOp.c_code()will be ignored.If
Op.make_node()is not defined, theOp.itypesandOp.otypesare used by theOp’sOp.make_node()method to implement the functionality ofOp.make_node()method mentioned above.
Op’s auxiliary methods#
There are other methods that can be optionally defined by the Op:
Op.__eq__()andOp.__hash__()define respectivelly equality between twoOps and the hash of anOpinstance. They will be used during the rewriting phase to merge nodes that are doing equivalent computations (same inputs, same operation). TwoOps that are equal accordingOp.__eq__()should return the same output when they are applied on the same inputs.The
Op.__props__attribute lists the properties that influence how the computation is performed. Usually these are set inOp.__init__(). It must be a tuple. If you don’t have any properties, then you should set this attribute to the empty tuple().
Op.__props__enables the automatic generation of appropriateOp.__eq__()andOp.__hash__(). Given the method__eq__(), automatically generated fromOp.__props__, twoOps will be equal if they have the same values for all the properties listed inOp.__props__. Given to the methodOp.__hash__()automatically generated fromOp.__props__, twoOps will be have the same hash if they have the same values for all the properties listed inOp.__props__.Op.__props__will also generate a suitableOp.__str__()for yourOp.The
Op.infer_shape()method allows anOpto infer the shape of its output variables without actually computing them. It takes as inputfgraph, aFunctionGraph;node, a reference to theOp’sApplynode; and a list ofVariabless (e.g.i0_shape,i1_shape, …) which are the dimensions of theOpinputVariables.Op.infer_shape()returns a list where each element is a tuple representing the shape of one output. This could be helpful if one only needs the shape of the output instead of the actual outputs, which can be useful, for instance, for rewriting procedures.The
Op.grad()method is required if you want to differentiate some cost whose expression includes yourOp. The gradient may be specified symbolically in this method. It takes two argumentsinputsandoutput_gradients, which are both lists ofVariables, and those must be operated on using Aesara’s symbolic language. TheOp.grad()method must return a list containing oneVariablefor each input. Each returnedVariablerepresents the gradient with respect to that input computed based on the symbolic gradients with respect to each output. If the output is not differentiable with respect to an input then this method should be defined to return a variable of typeNullTypefor that input. Likewise, if you have not implemented the gradient computation for some input, you may return a variable of typeNullTypefor that input. Please refer toOp.grad()for a more detailed view.The
Op.R_op()method is needed if you wantaesara.gradient.Rop()to work with yourOp. This function implements the application of the R-operator on the function represented by yourOp. Let assume that function is, with input
, applying the R-operator means computing the Jacobian of
and right-multiplying it by
, the evaluation point, namely:
.
The optional boolean
check_inputattribute is used to specify if you want the types used in yourCOpto check their inputs in theirCOp.c_code(). It can be used to speed up compilation, reduce overhead (particularly for scalars) and reduce the number of generated C files.
Example: Op definition#
import aesara
from aesara.graph.op import Op
from aesara.graph.basic import Apply
class DoubleOp1(Op):
__props__ = ()
def make_node(self, x):
x = aesara.tensor.as_tensor_variable(x)
# Note: using x_.type() is dangerous, as it copies x's broadcasting
# behaviour
return Apply(self, [x], [x.type()])
def perform(self, node, inputs, output_storage):
x = inputs[0]
z = output_storage[0]
z[0] = x * 2
def infer_shape(self, fgraph, node, i0_shapes):
return i0_shapes
def grad(self, inputs, output_grads):
return [output_grads[0] * 2]
def R_op(self, inputs, eval_points):
# R_op can receive None as eval_points.
# That mean there is no diferientiable path through that input
# If this imply that you cannot compute some outputs,
# return None for those.
if eval_points[0] is None:
return eval_points
return self.grad(inputs, eval_points)
doubleOp1 = DoubleOp1()
#Using itypes and otypes
class DoubleOp2(Op):
__props__ = ()
itypes = [aesara.tensor.dmatrix]
otypes = [aesara.tensor.dmatrix]
def perform(self, node, inputs, output_storage):
x = inputs[0]
z = output_storage[0]
z[0] = x * 2
def infer_shape(self, fgraph, node, i0_shapes):
return i0_shapes
def grad(self, inputs, output_grads):
return [output_grads[0] * 2]
def R_op(self, inputs, eval_points):
# R_op can receive None as eval_points.
# That mean there is no diferientiable path through that input
# If this imply that you cannot compute some outputs,
# return None for those.
if eval_points[0] is None:
return eval_points
return self.grad(inputs, eval_points)
doubleOp2 = DoubleOp2()
At a high level, the code fragment declares a class (e.g., DoubleOp1) and then
creates one instance of it (e.g., doubleOp1).
We often gloss over this distinction, but will be precise here:
doubleOp1 (the instance) is an Op, not DoubleOp1 (the class which is a
subclass of Op). You can call doubleOp1(tensor.vector()) on a
Variable to build an expression, and in the expression there will be
a .op attribute that refers to doubleOp1.
The make_node method creates a node to be included in the expression graph.
It runs when we apply our Op (doubleOp1) to the Variable (x), as
in doubleOp1(tensor.vector()).
When an Op has multiple inputs, their order in the inputs argument to Apply
is important: Aesara will call make_node(*inputs) to copy the graph,
so it is important not to change the semantics of the expression by changing
the argument order.
All the inputs and outputs arguments to Apply must be Variables.
A common and easy way to ensure inputs are variables is to run them through
as_tensor_variable. This function leaves TensorType variables alone, raises
an error for non-TensorType variables, and copies any numpy.ndarray into
the storage for a TensorType Constant. The make_node() method dictates the
appropriate Type for all output variables.
The perform() method implements the Op’s mathematical logic in Python.
The inputs (here x) are passed by value, but a single output is returned
indirectly as the first element of single-element lists. If doubleOp1 had
a second output, it would be stored in output_storage[1][0].
In some execution modes, the output storage might contain the return value of
a previous call. That old value can be reused to avoid memory re-allocation,
but it must not influence the semantics of the Op output.
You can try the new Op as follows:
import numpy as np
import aesara
x = aesara.tensor.matrix()
f = aesara.function([x], DoubleOp1()(x))
inp = np.random.random_sample((5, 4))
out = f(inp)
assert np.allclose(inp * 2, out)
print(inp)
print(out)
[[ 0.08257206 0.34308357 0.5288043 0.06582951]
[ 0.65977826 0.10040307 0.5402353 0.55472296]
[ 0.82358552 0.29502171 0.97387481 0.0080757 ]
[ 0.77327215 0.65401857 0.76562992 0.94145702]
[ 0.8452076 0.30500101 0.88430501 0.95818655]]
[[ 0.16514411 0.68616713 1.0576086 0.13165902]
[ 1.31955651 0.20080613 1.08047061 1.10944593]
[ 1.64717104 0.59004341 1.94774962 0.0161514 ]
[ 1.5465443 1.30803715 1.53125983 1.88291403]
[ 1.6904152 0.61000201 1.76861002 1.9163731 ]]
import numpy as np
import aesara
x = aesara.tensor.matrix()
f = aesara.function([x], DoubleOp2()(x))
inp = np.random.random_sample((5, 4))
out = f(inp)
assert np.allclose(inp * 2, out)
print(inp)
print(out)
[[ 0.02443785 0.67833979 0.91954769 0.95444365]
[ 0.60853382 0.7770539 0.78163219 0.92838837]
[ 0.04427765 0.37895602 0.23155797 0.4934699 ]
[ 0.20551517 0.7419955 0.34500905 0.49347629]
[ 0.24082769 0.49321452 0.24566545 0.15351132]]
[[ 0.04887571 1.35667957 1.83909538 1.90888731]
[ 1.21706764 1.55410779 1.56326439 1.85677674]
[ 0.08855531 0.75791203 0.46311594 0.9869398 ]
[ 0.41103034 1.48399101 0.69001811 0.98695258]
[ 0.48165539 0.98642904 0.4913309 0.30702264]]
Example: __props__ definition#
We can modify the previous piece of code in order to demonstrate
the usage of the __props__ attribute.
We create an Op that takes a variable x and returns a*x+b.
We want to say that two such Ops are equal when their values of a
and b are equal.
import aesara
from aesara.graph.op import Op
from aesara.graph.basic import Apply
class AXPBOp(Op):
"""
This creates an Op that takes x to a*x+b.
"""
__props__ = ("a", "b")
def __init__(self, a, b):
self.a = a
self.b = b
super().__init__()
def make_node(self, x):
x = aesara.tensor.as_tensor_variable(x)
return Apply(self, [x], [x.type()])
def perform(self, node, inputs, output_storage):
x = inputs[0]
z = output_storage[0]
z[0] = self.a * x + self.b
def infer_shape(self, fgraph, node, i0_shapes):
return i0_shapes
def grad(self, inputs, output_grads):
return [self.a * output_grads[0]]
The use of __props__ saves
the user the trouble of implementing __eq__() and __hash__()
manually. It also generates a default __str__() method that prints the
attribute names and their values.
We can test this by running the following segment:
mult4plus5op = AXPBOp(4, 5)
another_mult4plus5op = AXPBOp(4, 5)
mult2plus3op = AXPBOp(2, 3)
assert mult4plus5op == another_mult4plus5op
assert mult4plus5op != mult2plus3op
x = aesara.tensor.matrix()
f = aesara.function([x], mult4plus5op(x))
g = aesara.function([x], mult2plus3op(x))
inp = np.random.random_sample((5, 4)).astype(np.float32)
assert np.allclose(4 * inp + 5, f(inp))
assert np.allclose(2 * inp + 3, g(inp))
How To Test it#
Aesara has some functionalities to simplify testing. These help test the
Op.infer_shape(), Op.grad() and Op.R_op() methods. Put the following code
in a file and execute it with the pytest program.
Basic Tests#
Basic tests are done by you just by using the Op and checking that it
returns the right answer. If you detect an error, you must raise an
exception. You can use the assert keyword to automatically raise an
AssertionError.
import numpy as np
import aesara
from tests import unittest_tools as utt
class TestDouble(utt.InferShapeTester):
def setup_method(self):
super().setup_method()
self.op_class = DoubleOp
self.op = DoubleOp()
def test_basic(self):
rng = np.random.default_rng(utt.fetch_seed())
x = aesara.tensor.matrix()
f = aesara.function([x], self.op(x))
inp = np.asarray(rng.random((5, 4)), dtype=aesara.config.floatX)
out = f(inp)
# Compare the result computed to the expected value.
utt.assert_allclose(inp * 2, out)
We call utt.assert_allclose(expected_value, value) to compare
NumPy ndarray.This raise an error message with more information. Also,
the default tolerance can be changed with the Aesara flags
config.tensor__cmp_sloppy that take values in 0, 1 and 2. The
default value do the most strict comparison, 1 and 2 make less strict
comparison.
Testing the Op.infer_shape()#
When a class inherits from the InferShapeTester class, it gets the
InferShapeTester._compile_and_check() method that tests the Op.infer_shape()
method. It tests that the Op gets rewritten out of the graph if only
the shape of the output is needed and not the output
itself. Additionally, it checks that the rewritten graph computes
the correct shape, by comparing it to the actual shape of the computed
output.
InferShapeTester._compile_and_check() compiles an Aesara function. It takes as
parameters the lists of input and output Aesara variables, as would be
provided to aesara.function(), and a list of real values to pass to the
compiled function. It also takes the Op class as a parameter
in order to verify that no instance of it appears in the shape-optimized graph.
If there is an error, the function raises an exception. If you want to
see it fail, you can implement an incorrect Op.infer_shape().
When testing with input values with shapes that take the same value
over different dimensions (for instance, a square matrix, or a tensor3
with shape (n, n, n), or (m, n, m)), it is not possible to detect if
the output shape was computed correctly, or if some shapes with the
same value have been mixed up. For instance, if the Op.infer_shape() uses
the width of a matrix instead of its height, then testing with only
square matrices will not detect the problem. This is why the
InferShapeTester._compile_and_check() method prints a warning in such a case. If
your Op works only with such matrices, you can disable the warning with the
warn=False parameter.
from aesara.configdefaults import config
from tests import unittest_tools as utt
class TestDouble(utt.InferShapeTester):
# [...] as previous tests.
def test_infer_shape(self):
rng = np.random.default_rng(utt.fetch_seed())
x = aesara.tensor.matrix()
self._compile_and_check(
[x], # aesara.function inputs
[self.op(x)], # aesara.function outputs
# Always use not square matrix!
# inputs data
[np.asarray(rng.random((5, 4)), dtype=config.floatX)],
# Op that should be removed from the graph.
self.op_class,
)
Testing the gradient#
The function verify_grad verifies the gradient of an Op or Aesara
graph. It compares the analytic (symbolically computed) gradient and the numeric
gradient (computed through the Finite Difference Method).
If there is an error, the function raises an exception. If you want to see it fail, you can implement an incorrect gradient (for instance, by removing the multiplication by 2).
def test_grad(self):
rng = np.random.default_rng(utt.fetch_seed())
tests.unittest_tools.verify_grad(
self.op,
[rng.random((5, 7, 2))]
)
Testing the Rop#
The class RopLop_checker defines the functions
RopLop_checker.check_mat_rop_lop(), RopLop_checker.check_rop_lop() and
RopLop_checker.check_nondiff_rop(). These allow to test the
implementation of the Rop() method of a particular Op.
For instance, to verify the Rop() method of the DoubleOp, you can use this:
import numpy
import tests
from tests.test_rop import RopLop_checker
class TestDoubleRop(RopLop_checker):
def setUp(self):
super(TestDoubleRop, self).setUp()
def test_double_rop(self):
self.check_rop_lop(DoubleRop()(self.x), self.in_shape)
Running Your Tests#
To perform your tests, simply run pytest.
In-file#
One may also add a block of code similar to the following at the end
of the file containing a specific test of interest and run the
file. In this example, the test TestDoubleRop in the class
test_double_op would be performed.
if __name__ == '__main__':
t = TestDoubleRop("test_double_rop")
t.setUp()
t.test_double_rop()
We recommend that when we execute a file, we run all tests in that file. This can be done by adding this at the end of your test files:
if __name__ == '__main__':
unittest.main()
Exercise#
Run the code of the DoubleOp example above.
Modify and execute to compute: x * y.
Modify and execute the example to return two outputs: x + y and jx - yj.
You can omit the Rop() functions. Try to implement the testing apparatus
described above.
(Notice that Aesara’s current elemwise fusion rewrite is only applicable to computations involving a single output. Hence, to gain efficiency over the basic solution that is asked here, the two operations would have to be jointly rewritten explicitly in the code.)
Random numbers in tests#
Making tests errors more reproducible is a good practice. To make tests more reproducible, one needs a way to get the same random numbers. This can be done by seeding NumPy’s random number generator.
For convenience, the classes InferShapeTester and RopLop_checker
already do this for you. If you implement your own setUp() method,
don’t forget to call the parent setUp() method.
as_op()#
as_op() is a Python decorator that converts a Python function into a
basic Aesara Op that will call the supplied function during execution.
This isn’t the recommended way to build an Op, but allows for a quick
implementation.
It takes an optional Op.infer_shape() parameter that must have this
signature:
def infer_shape(fgraph, node, input_shapes):
# ...
return output_shapes
- :obj:`input_shapes` and :obj:`output_shapes` are lists of tuples that
represent the shape of the corresponding inputs/outputs, and :obj:`fgraph`
is a :class:`FunctionGraph`.
Warning
Not providing a Op.infer_shape() prevents shape-related
rewrites from working with this Op. For example
your_op(inputs, ...).shape will need the Op to be executed just
to get the shape.
Note
As no grad is defined, this means you won’t be able to
differentiate paths that include this Op.
Note
It converts the Python function to a callable object that takes as inputs Aesara variables that were declared.
Note
The python function wrapped by the as_op() decorator needs to return a new
data allocation, no views or in place modification of the input.
as_op() Example#
import aesara
import aesara.tensor as at
import numpy as np
from aesara import function
from aesara.compile.ops import as_op
def infer_shape_numpy_dot(fgraph, node, input_shapes):
ashp, bshp = input_shapes
return [ashp[:-1] + bshp[-1:]]
@as_op(itypes=[at.matrix, at.matrix],
otypes=[at.matrix], infer_shape=infer_shape_numpy_dot)
def numpy_dot(a, b):
return np.dot(a, b)
You can try it as follows:
x = at.matrix()
y = at.matrix()
f = function([x, y], numpy_dot(x, y))
inp1 = np.random.random_sample((5, 4))
inp2 = np.random.random_sample((4, 7))
out = f(inp1, inp2)
Documentation and Coding Style#
Please always respect the Requirements for Quality Contributions or your contribution will not be accepted.
NanGuardMode and AllocEmpty#
NanGuardMode help users find where in the graph NaN appear. But
sometimes, we want some variables to not be checked. For example, in
the old GPU back-end, we used a float32 CudaNdarray to store the MRG
random number generator state (they are integers). So if NanGuardMode
checked it, it would generate a false positive. Another case is related to
AllocEmpty or some computations on it (like done by Scan).
You can tell NanGuardMode to do not check a variable with:
variable.tag.nan_guard_mode_check. Also, this tag automatically
follows that variable during rewriting. This mean if you tag a
variable that get replaced by an inplace version, it will keep that
tag.
Final Note#
The section Other Ops includes more instructions for the following specific cases:
