Ops#
An Op is a graph object that defines and performs computations in a graph.
It has to define the following methods.
- make_node(*inputs)#
This method is responsible for creating output
Variables of a suitable symbolicTypeto serve as the outputs of thisOp’s application. TheVariables found in*inputsmust be operated on using Aesara’s symbolic language to compute the symbolic outputVariables. This method should put these outputs into anApplyinstance, and return theApplyinstance.This method creates an
Applynode representing the application of theOpon the inputs provided. If theOpcannot be applied to these inputs, it must raise an appropriate exception.The inputs of the
Applyinstance returned by this call must be ordered correctly: a subsequentself.make_node(*apply.inputs)must produce something equivalent to the firstapply.
- perform(node, inputs, output_storage)#
This method computes the function associated to this
Op.nodeis anApplynode created by theOp’sOp.make_node()method.inputsis a list of references to data to operate on using non-symbolic statements, (i.e., statements in Python, NumPy).output_storageis a list of storage cells where the variables of the computation must be put.More specifically:
node: This is a reference to anApplynode which was previously obtained via theOp.make_node()method. It is typically not used in simpleOps, but it contains symbolic information that could be required for complexOps.inputs: This is a list of data from which the values stored inoutput_storageare to be computed using non-symbolic language.output_storage: This is a list of storage cells where the output is to be stored. A storage cell is a one-element list. It is forbidden to change the length of the list(s) contained inoutput_storage. There is one storage cell for each output of theOp.The data put in
output_storagemust match the type of the symbolic output. This is a situation where thenodeargument can come in handy.A function
Modemay allowoutput_storageelements to persist between evaluations, or it may resetoutput_storagecells to hold a value ofNone. It can also pre-allocate some memory for theOpto use. This feature can allowOp.perform()to reuse memory between calls, for example. If there is something preallocated in theoutput_storage, it will be of the good dtype, but can have the wrong shape and have any stride pattern.
This method must be determined by the inputs. That is to say, if it is evaluated once on inputs A and returned B, then if ever inputs C, equal to A, are presented again, then outputs equal to B must be returned again.
You must be careful about aliasing outputs to inputs, and making modifications to any of the inputs. See Views and inplace operations before writing a
Op.perform()implementation that does either of these things.
- __eq__(other)#
otheris also anOp.Returning
Truehere is a promise to the rewrite system that the otherOpwill produce exactly the same graph effects (e.g. from itsOp.perform()) as this one, given identical inputs. This means it will produce the same output values, it will destroy the same inputs (sameOp.destroy_map), and will alias outputs to the same inputs (sameOp.view_map). For more details, see Views and inplace operations.Note
If you set
__props__, this will be automatically generated.
- __hash__()#
If two
Opinstances compare equal, then they must return the same hash value.Equally important, this hash value must not change during the lifetime of self.
Opinstances should be immutable in this sense.
Note
If you set Op.__props__, this will be automatically generated.
Optional methods or attributes#
- __props__#
Default: Undefined
Must be a tuple. Lists the name of the attributes which influence the computation performed. This will also enable the automatic generation of appropriate
__eq__,__hash__and__str__methods. Should be set to()if you have no attributes that are relevant to the computation to generate the methods.New in version 0.7.
- default_output#
Default: None
If this member variable is an integer, then the default implementation of
__call__will returnnode.outputs[self.default_output], wherenodewas returned byOp.make_node(). Otherwise, the entire list of outputs will be returned, unless it is of length 1, where the single element will be returned by itself.
- make_thunk(node, storage_map, compute_map, no_recycling, impl=None)#
This function must return a thunk, that is a zero-arguments function that encapsulates the computation to be performed by this
Opon the arguments of the node.- Parameters:
node –
Applyinstance The node for which a thunk is requested.storage_map – dict of lists This maps variables to a one-element lists holding the variable’s current value. The one-element list acts as pointer to the value and allows sharing that “pointer” with other nodes and instances.
compute_map – dict of lists This maps variables to one-element lists holding booleans. If the value is 0 then the variable has not been computed and the value should not be considered valid. If the value is 1 the variable has been computed and the value is valid. If the value is 2 the variable has been garbage-collected and is no longer valid, but shouldn’t be required anymore for this call.
no_recycling – WRITEME WRITEME
impl – None, ‘c’ or ‘py’ Which implementation to use.
The returned function must ensure that is sets the computed variables as computed in the
compute_map.Defining this function removes the requirement for
perform()or C code, as you will define the thunk for the computation yourself.
- __call__(*inputs, **kwargs)#
By default this is a convenience function which calls
make_node()with the supplied arguments and returns the result indexed bydefault_output. This can be overridden by subclasses to do anything else, but must return either an AesaraVariableor a list ofVariables.If you feel the need to override
__call__to change the graph based on the arguments, you should instead create a function that will use yourOpand build the graphs that you want and call that instead of theOpinstance directly.
- infer_shape(fgraph, node, shapes)#
This function is needed for shape rewrites.
shapesis a list with one tuple for each input of theApplynode (which corresponds to the inputs of theOp). Each tuple contains as many elements as the number of dimensions of the corresponding input. The value of each element is the shape (number of items) along the corresponding dimension of that specific input.While this might sound complicated, it is nothing more than the shape of each input as symbolic variables (one per dimension).
The function should return a list with one tuple for each output. Each tuple should contain the corresponding output’s computed shape.
Implementing this method will allow Aesara to compute the output’s shape without computing the output itself, potentially sparing you a costly recomputation.
- flops(inputs, outputs)#
It is only used to have more information printed by the memory profiler. It makes it print the mega flops and giga flops per second for each apply node. It takes as inputs two lists: one for the inputs and one for the outputs. They contain tuples that are the shapes of the corresponding inputs/outputs.
- __str__()#
This allows you to specify a more informative string representation of your
Op. If anOphas parameters, it is highly recommended to have the__str__method include the name of theOpand theOp’s parameters’ values.Note
If you set
__props__, this will be automatically generated. You can still override it for custom output.
- do_constant_folding(fgraph, node)#
Default: Return
TrueBy default when rewrites are enabled, we remove during function compilation
Applynodes whose inputs are all constants. We replace theApplynode with an Aesara constant variable. This way, theApplynode is not executed at each function call. If you want to force the execution of anOpduring the function call, make do_constant_folding return False.As done in the Alloc
Op, you can return False only in some cases by analyzing the graph from the node parameter.
- debug_perform(node, inputs, output_storage)#
Undefined by default.
If you define this function then it will be used instead of C code or
Op.perform()to do the computation while debugging (currently DebugMode, but others may also use it in the future). It has the same signature and contract asOp.perform().This enables
Ops that cause trouble with DebugMode with their normal behaviour to adopt a different one when run under that mode. If yourOpdoesn’t have any problems, don’t implement this.
If you want your Op to work with aesara.gradient.grad() you also
need to implement the functions described below.
Gradient#
These are the function required to work with aesara.gradient.grad().
- grad(inputs, output_gradients)#
If the
Opbeing defined is differentiable, its gradient may be specified symbolically in this method. Bothinputsandoutput_gradientsare lists of symbolic AesaraVariables and those must be operated on using Aesara’s symbolic language. TheOp.grad()method must return a list containing oneVariablefor each input. Each returnedVariablerepresents the gradient with respect to that input computed based on the symbolic gradients with respect to each output.If the output is not differentiable with respect to an input then this method should be defined to return a variable of type
NullTypefor that input. Likewise, if you have not implemented the gradient computation for some input, you may return a variable of typeNullTypefor that input.aesara.gradientcontains convenience methods that can construct the variable for you:aesara.gradient.grad_undefined()andaesara.gradient.grad_not_implemented(), respectively.If an element of
output_gradientis of typeaesara.gradient.DisconnectedType, it means that the cost is not a function of this output. If any of theOp’s inputs participate in the computation of only disconnected outputs, thenOp.grad()should returnDisconnectedTypevariables for those inputs.If the
Op.grad()method is not defined, then Aesara assumes it has been forgotten. Symbolic differentiation will fail on a graph that includes thisOp.It must be understood that the
Op.grad()method is not meant to return the gradient of theOp’s output.aesara.grad()computes gradients;Op.grad()is a helper function that computes terms that appear in gradients.If an
Ophas a single vector-valued outputyand a single vector-valued inputx, then theOp.grad()method will be passedxand a second vectorz. DefineJto be the Jacobian ofywith respect tox. TheOp.grad()method should returndot(J.T,z). Whenaesara.grad()calls theOp.grad()method, it will setzto be the gradient of the costCwith respect toy. If thisOpis the onlyOpthat acts onx, thendot(J.T,z)is the gradient of C with respect tox. If there are otherOps that act onx,aesara.grad()will have to add up the terms ofx’s gradient contributed by the otherOp.grad()method.In practice, an
Op’s input and output are rarely implemented as single vectors. Even if anOp’s output consists of a list containing a scalar, a sparse matrix, and a 4D tensor, you can think of these objects as being formed by rearranging a vector. Likewise for the input. In this view, the values computed by theOp.grad()method still represent a Jacobian-vector product.In practice, it is probably not a good idea to explicitly construct the Jacobian, which might be very large and very sparse. However, the returned value should be equal to the Jacobian-vector product.
So long as you implement this product correctly, you need not understand what
aesara.gradient.grad()is doing, but for the curious the mathematical justification is as follows:In essence, the
Op.grad()method must simply implement through symbolicVariables and operations the chain rule of differential calculus. The chain rule is the mathematical procedure that allows one to calculate the total derivative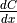 of the
final scalar symbolic
of the
final scalar symbolic VariableCwith respect to a primitive symbolicVariablex found in the listinputs. TheOp.grad()method does this usingoutput_gradientswhich provides the total derivative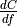 of
of Cwith respect to a symbolicVariablethat is returned by theOp(this is provided inoutput_gradients), as well as the knowledge of the total derivative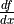 of the latter with respect to the
primitive
of the latter with respect to the
primitive Variable(this has to be computed).In mathematics, the total derivative of a scalar variable
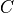 with
respect to a vector of scalar variables
with
respect to a vector of scalar variables  , i.e. the gradient, is
customarily represented as the row vector of the partial
derivatives, whereas the total derivative of a vector of scalar
variables
, i.e. the gradient, is
customarily represented as the row vector of the partial
derivatives, whereas the total derivative of a vector of scalar
variables 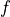 with respect to another
with respect to another  , is customarily
represented by the matrix of the partial derivatives, i.e. the
Jacobian matrix. In this convenient setting, the chain rule
says that the gradient of the final scalar variable
, is customarily
represented by the matrix of the partial derivatives, i.e. the
Jacobian matrix. In this convenient setting, the chain rule
says that the gradient of the final scalar variable 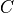 with
respect to the primitive scalar variables in
with
respect to the primitive scalar variables in  through those in
through those in
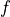 is simply given by the matrix product:
is simply given by the matrix product:
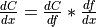 .
.Here, the chain rule must be implemented in a similar but slightly more complex setting: Aesara provides in the list
output_gradientsone gradient for each of theVariables returned by theOp. Where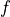 is one such particular
is one such particular Variable, the corresponding gradient found inoutput_gradientsand representing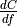 is provided with a shape
similar to
is provided with a shape
similar to 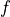 and thus not necessarily as a row vector of scalars.
Furthermore, for each
and thus not necessarily as a row vector of scalars.
Furthermore, for each Variable of the
of the Op’s list of input variablesinputs, the returned gradient representing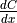 must have a shape similar to that of
must have a shape similar to that of Variablex.If the output list of the
Opis![[f_1, ... f_n]](../../_images/math/9119289ee92e7da53ca943b6855b25ab592004ab.png) , then the
list
, then the
list output_gradientsis![[grad_{f_1}(C), grad_{f_2}(C),
... , grad_{f_n}(C)]](../../_images/math/e8dfb821739d6c5e2b714bf5c6e4533ff54ace4e.png) . If
. If inputsconsists of the list![[x_1, ..., x_m]](../../_images/math/803c4d7c98916a5302ac241179722ff5334f21f0.png) , then
, then Op.gradshould return the list![[grad_{x_1}(C), grad_{x_2}(C), ..., grad_{x_m}(C)]](../../_images/math/3d9b397a200bd0333058ec1cfdf0822eef153728.png) , where
, where
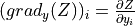 (and
(and
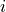 can stand for multiple dimensions).
can stand for multiple dimensions).In other words,
Op.grad()does not return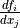 , but instead the appropriate dot product specified by the
chain rule:
, but instead the appropriate dot product specified by the
chain rule: 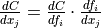 . Both the partial differentiation and the
multiplication have to be performed by
. Both the partial differentiation and the
multiplication have to be performed by Op.grad().Aesara currently imposes the following constraints on the values returned by the
Op.grad()method:They must be
Variableinstances.When they are types that have dtypes, they must never have an integer dtype.
The output gradients passed to
Op.grad()will also obey these constraints.Integers are a tricky subject. Integers are the main reason for having
DisconnectedType,NullTypeor zero gradient. When you have an integer as an argument to yourOp.grad()method, recall the definition of a derivative to help you decide what value to return: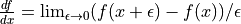 .
.Suppose your function f has an integer-valued output. For most functions you’re likely to implement in Aesara, this means your gradient should be zero, because
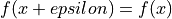 for almost all
for almost all
 . (The only other option is that the gradient could be undefined,
if your function is discontinuous everywhere, like the rational
indicator function)
. (The only other option is that the gradient could be undefined,
if your function is discontinuous everywhere, like the rational
indicator function)Suppose your function
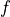 has an integer-valued input. This is a
little trickier, because you need to think about what you mean
mathematically when you make a variable integer-valued in
Aesara. Most of the time in machine learning we mean “
has an integer-valued input. This is a
little trickier, because you need to think about what you mean
mathematically when you make a variable integer-valued in
Aesara. Most of the time in machine learning we mean “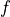 is a
function of a real-valued
is a
function of a real-valued  , but we are only going to pass in
integer-values of
, but we are only going to pass in
integer-values of  ”. In this case,
”. In this case, 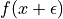 exists, so the
gradient through
exists, so the
gradient through 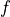 should be the same whether
should be the same whether  is an integer or a
floating point variable. Sometimes what we mean is “
is an integer or a
floating point variable. Sometimes what we mean is “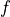 is a function
of an integer-valued
is a function
of an integer-valued  , and
, and 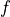 is only defined where
is only defined where  is an
integer.” Since
is an
integer.” Since 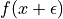 doesn’t exist, the gradient is
undefined. Finally, many times in Aesara, integer valued inputs
don’t actually affect the elements of the output, only its shape.
doesn’t exist, the gradient is
undefined. Finally, many times in Aesara, integer valued inputs
don’t actually affect the elements of the output, only its shape.If your function
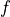 has both an integer-valued input and an
integer-valued output, then both rules have to be combined:
has both an integer-valued input and an
integer-valued output, then both rules have to be combined:If
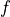 is defined at
is defined at 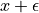 , then the input gradient is
defined. Since
, then the input gradient is
defined. Since 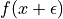 would be equal to
would be equal to 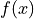 almost
everywhere, the gradient should be zero (first rule).
almost
everywhere, the gradient should be zero (first rule).If
 is only defined where
is only defined where  is an integer, then the gradient
is undefined, regardless of what the gradient with respect to the
output is.
is an integer, then the gradient
is undefined, regardless of what the gradient with respect to the
output is.
Examples:
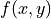 is a dot product between
is a dot product between  and
and 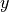 .
.  and
and 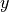 are integers.
Since the output is also an integer,
are integers.
Since the output is also an integer, 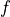 is a step function.
Its gradient is zero almost everywhere, so
is a step function.
Its gradient is zero almost everywhere, so Op.grad()should return zeros in the shape of and
and 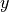 .
.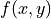 is a dot product between
is a dot product between  and
and 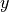 .
.  is floating point and
is floating point and 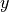 is an integer. In this case the output is
floating point. It doesn’t matter that
is an integer. In this case the output is
floating point. It doesn’t matter that 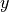 is an integer. We
consider
is an integer. We
consider 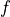 to still be defined at
to still be defined at 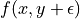 . The
gradient is exactly the same as if
. The
gradient is exactly the same as if 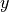 were floating point.
were floating point.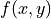 is the argmax of
is the argmax of  along axis
along axis 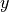 . The
gradient with respect to
. The
gradient with respect to 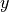 is undefined, because
is undefined, because 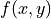 is
not defined for floating point
is
not defined for floating point 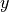 . How could you take an argmax
along a fractional axis? The gradient with respect to
. How could you take an argmax
along a fractional axis? The gradient with respect to  is 0,
because
is 0,
because 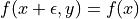 almost everywhere.
almost everywhere.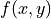 is a vector with
is a vector with 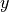 elements, each of which taking on
the value
elements, each of which taking on
the value  The
The Op.grad()method should returnDisconnectedTypefor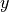 , because the elements of
, because the elements of 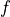 don’t depend on
don’t depend on 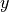 . Only the shape of
. Only the shape of 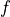 depends on
depends on
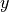 . You probably also want to implement a connection_pattern method to encode this.
. You probably also want to implement a connection_pattern method to encode this.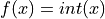 converts float
converts float  into an integer.
into an integer. 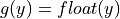 converts an integer
converts an integer 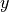 into a float. If the final cost
into a float. If the final cost 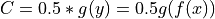 , then the gradient with respect to
, then the gradient with respect to 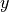 will be 0.5,
even if
will be 0.5,
even if 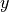 is an integer. However, the gradient with respect to
is an integer. However, the gradient with respect to  will be
0, because the output of
will be
0, because the output of 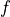 is integer-valued.
is integer-valued.
- connection_pattern(node):
Sometimes needed for proper operation of
aesara.gradient.grad().Returns a list of list of booleans.
Op.connection_pattern[input_idx][output_idx]is true if the elements ofinputs[input_idx]have an effect on the elements ofoutputs[output_idx].The
nodeparameter is needed to determine the number of inputs. SomeOps such asSubtensortake a variable number of inputs.If no connection_pattern is specified,
aesara.gradient.grad()will assume that all inputs have some elements connected to some elements of all outputs.This method conveys two pieces of information that are otherwise not part of the Aesara graph:
Which of the
Op’s inputs are truly ancestors of each of theOp’s outputs. Suppose anOphas two inputs, and
and 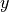 , and
outputs
, and
outputs 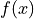 and
and 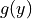 .
. 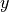 is not really an ancestor of
is not really an ancestor of 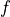 , but
it appears to be so in the Aesara graph.
, but
it appears to be so in the Aesara graph.Whether the actual elements of each input/output are relevant to a computation. For example, the shape
Opdoes not read its input’s elements, only its shape metadata.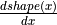 should thus raise
a disconnected input exception (if these exceptions are enabled).
As another example, the elements of the
should thus raise
a disconnected input exception (if these exceptions are enabled).
As another example, the elements of the AllocOp’s outputs are not affected by the shape arguments to theAllocOp.
Failing to implement this function for an
Opthat needs it can result in two types of incorrect behavior:aesara.gradient.grad()erroneously raising aTypeErrorreporting that a gradient is undefined.aesara.gradient.grad()failing to raise aValueErrorreporting that an input is disconnected.
Even if connection_pattern is not implemented correctly, if
aesara.gradient.grad()returns an expression, that expression will be numerically correct.
- R_op(inputs, eval_points)#
Optional, to work with
aesara.gradient.R_op().This function implements the application of the R-operator on the function represented by your
Op. Let assume that function is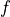 ,
with input
,
with input  , applying the R-operator means computing the
Jacobian of
, applying the R-operator means computing the
Jacobian of 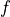 and right-multiplying it by
and right-multiplying it by  , the evaluation
point, namely:
, the evaluation
point, namely: 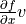 .
.inputsare the symbolic variables corresponding to the value of the input where you want to evaluate the Jacobian, andeval_pointsare the symbolic variables corresponding to the value you want to right multiply the Jacobian with.Same conventions as for the
Op.grad()method hold. If yourOpis not differentiable, you can return None. Note that in contrast to the methodOp.grad(), forOp.R_op()you need to return the same number of outputs as there are outputs of theOp. You can think of it in the following terms. You have all your inputs concatenated into a single vector . You do the same with the evaluation
points (which are as many as inputs and of the shame shape) and obtain
another vector
. You do the same with the evaluation
points (which are as many as inputs and of the shame shape) and obtain
another vector  . For each output, you reshape it into a vector,
compute the Jacobian of that vector with respect to
. For each output, you reshape it into a vector,
compute the Jacobian of that vector with respect to  and
multiply it by
and
multiply it by  . As a last step you reshape each of these
vectors you obtained for each outputs (that have the same shape as
the outputs) back to their corresponding shapes and return them as the
output of the
. As a last step you reshape each of these
vectors you obtained for each outputs (that have the same shape as
the outputs) back to their corresponding shapes and return them as the
output of the Op.R_op()method.
