Guide#
The scan functions provides the basic functionality needed to do loops in Aesara. Scan comes with many whistles and bells, which we will introduce by way of examples.
Simple loop with accumulation: Computing 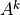 #
#
Assume that, given k you want to get A**k using a loop.
More precisely, if A is a tensor you want to compute
A**k elemwise. The python/numpy code might look like:
result = 1
for i in range(k):
result = result * A
There are three things here that we need to handle: the initial value
assigned to result, the accumulation of results in result, and
the unchanging variable A. Unchanging variables are passed to scan as
non_sequences. Initialization occurs in outputs_info, and the accumulation
happens automatically.
The equivalent Aesara code would be:
import aesara
import aesara.tensor as at
k = at.iscalar("k")
A = at.vector("A")
# Symbolic description of the result
result, updates = aesara.scan(fn=lambda prior_result, A: prior_result * A,
outputs_info=at.ones_like(A),
non_sequences=A,
n_steps=k)
# We only care about A**k, but scan has provided us with A**1 through A**k.
# Discard the values that we don't care about. Scan is smart enough to
# notice this and not waste memory saving them.
final_result = result[-1]
# compiled function that returns A**k
power = aesara.function(inputs=[A,k], outputs=final_result, updates=updates)
print(power(range(10),2))
print(power(range(10),4))
[ 0. 1. 4. 9. 16. 25. 36. 49. 64. 81.]
[ 0.00000000e+00 1.00000000e+00 1.60000000e+01 8.10000000e+01
2.56000000e+02 6.25000000e+02 1.29600000e+03 2.40100000e+03
4.09600000e+03 6.56100000e+03]
Let us go through the example line by line. What we did is first to
construct a function (using a lambda expression) that given prior_result and
A returns prior_result * A. The order of parameters is fixed by scan:
the output of the prior call to fn (or the initial value, initially)
is the first parameter, followed by all non-sequences.
Next we initialize the output as a tensor with same shape and dtype as A,
filled with ones. We give A to scan as a non sequence parameter and
specify the number of steps k to iterate over our lambda expression.
Scan returns a tuple containing our result (result) and a
dictionary of updates (empty in this case). Note that the result
is not a matrix, but a 3D tensor containing the value of A**k for
each step. We want the last value (after k steps) so we compile
a function to return just that. Note that there is a rewrite that
at compile time will detect that you are using just the last value of the
result and ensure that scan does not store all the intermediate values
that are used. So do not worry if A and k are large.
Iterating over the first dimension of a tensor: Calculating a polynomial#
In addition to looping a fixed number of times, scan can iterate over
the leading dimension of tensors (similar to Python’s for x in a_list).
The tensor(s) to be looped over should be provided to scan using the
sequence keyword argument.
Here’s an example that builds a symbolic calculation of a polynomial from a list of its coefficients:
import numpy
coefficients = aesara.tensor.vector("coefficients")
x = at.scalar("x")
max_coefficients_supported = 10000
# Generate the components of the polynomial
components, updates = aesara.scan(fn=lambda coefficient, power, free_variable: coefficient * (free_variable ** power),
outputs_info=None,
sequences=[coefficients, aesara.tensor.arange(max_coefficients_supported)],
non_sequences=x)
# Sum them up
polynomial = components.sum()
# Compile a function
calculate_polynomial = aesara.function(inputs=[coefficients, x], outputs=polynomial)
# Test
test_coefficients = numpy.asarray([1, 0, 2], dtype=numpy.float32)
test_value = 3
print(calculate_polynomial(test_coefficients, test_value))
print(1.0 * (3 ** 0) + 0.0 * (3 ** 1) + 2.0 * (3 ** 2))
19.0
19.0
There are a few things to note here.
First, we calculate the polynomial by first generating each of the coefficients, and then summing them at the end. (We could also have accumulated them along the way, and then taken the last one, which would have been more memory-efficient, but this is an example.)
Second, there is no accumulation of results, we can set outputs_info to None. This indicates
to scan that it doesn’t need to pass the prior result to fn.
The general order of function parameters to fn is:
sequences (if any), prior result(s) (if needed), non-sequences (if any)
Third, there’s a handy trick used to simulate python’s enumerate: simply include
aesara.tensor.arange to the sequences.
Fourth, given multiple sequences of uneven lengths, scan will truncate to the shortest of them. This makes it safe to pass a very long arange, which we need to do for generality, since arange must have its length specified at creation time.
Simple accumulation into a scalar, ditching lambda#
Although this example would seem almost self-explanatory, it stresses a
pitfall to be careful of: the initial output state that is supplied, that is
outputs_info, must be of a shape similar to that of the output variable
generated at each iteration and moreover, it must not involve an implicit
downcast of the latter.
import numpy as np
import aesara
import aesara.tensor as at
up_to = at.iscalar("up_to")
# define a named function, rather than using lambda
def accumulate_by_adding(arange_val, sum_to_date):
return sum_to_date + arange_val
seq = at.arange(up_to)
# An unauthorized implicit downcast from the dtype of 'seq', to that of
# 'at.as_tensor_variable(0)' which is of dtype 'int8' by default would occur
# if this instruction were to be used instead of the next one:
# outputs_info = at.as_tensor_variable(0)
outputs_info = at.as_tensor_variable(np.asarray(0, seq.dtype))
scan_result, scan_updates = aesara.scan(fn=accumulate_by_adding,
outputs_info=outputs_info,
sequences=seq)
triangular_sequence = aesara.function(inputs=[up_to], outputs=scan_result)
# test
some_num = 15
print(triangular_sequence(some_num))
print([n * (n + 1) // 2 for n in range(some_num)])
[ 0 1 3 6 10 15 21 28 36 45 55 66 78 91 105]
[0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105]
Another simple example#
Unlike some of the prior examples, this one is hard to reproduce except by using scan.
This takes a sequence of array indices, and values to place there, and a “model” output array (whose shape and dtype will be mimicked), and produces a sequence of arrays with the shape and dtype of the model, with all values set to zero except at the provided array indices.
location = at.imatrix("location")
values = at.vector("values")
output_model = at.matrix("output_model")
def set_value_at_position(a_location, a_value, output_model):
zeros = at.zeros_like(output_model)
zeros_subtensor = zeros[a_location[0], a_location[1]]
return at.set_subtensor(zeros_subtensor, a_value)
result, updates = aesara.scan(fn=set_value_at_position,
outputs_info=None,
sequences=[location, values],
non_sequences=output_model)
assign_values_at_positions = aesara.function(inputs=[location, values, output_model], outputs=result)
# test
test_locations = numpy.asarray([[1, 1], [2, 3]], dtype=numpy.int32)
test_values = numpy.asarray([42, 50], dtype=numpy.float32)
test_output_model = numpy.zeros((5, 5), dtype=numpy.float32)
print(assign_values_at_positions(test_locations, test_values, test_output_model))
[[[ 0. 0. 0. 0. 0.]
[ 0. 42. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]
[[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 50. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]]
This demonstrates that you can introduce new Aesara variables into a scan function.
Multiple outputs, several taps values - Recurrent Neural Network with Scan#
The examples above showed simple uses of scan. However, scan also supports referring not only to the prior result and the current sequence value, but also looking back more than one step.
This is needed, for example, to implement a RNN using scan. Assume that our RNN is defined as follows :
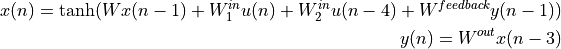
Note that this network is far from a classical recurrent neural network and might be useless. The reason we defined as such is to better illustrate the features of scan.
In this case we have a sequence over which we need to iterate u,
and two outputs x and y. To implement this with scan we first
construct a function that computes one iteration step :
def oneStep(u_tm4, u_t, x_tm3, x_tm1, y_tm1, W, W_in_1, W_in_2, W_feedback, W_out):
x_t = at.tanh(aesara.dot(x_tm1, W) + \
aesara.dot(u_t, W_in_1) + \
aesara.dot(u_tm4, W_in_2) + \
aesara.dot(y_tm1, W_feedback))
y_t = aesara.dot(x_tm3, W_out)
return [x_t, y_t]
As naming convention for the variables we used a_tmb to mean a at
t-b and a_tpb to be a at t+b.
Note the order in which the parameters are given, and in which the
result is returned. Try to respect chronological order among
the taps ( time slices of sequences or outputs) used. For scan is crucial only
for the variables representing the different time taps to be in the same order
as the one in which these taps are given. Also, not only taps should respect
an order, but also variables, since this is how scan figures out what should
be represented by what. Given that we have all
the Aesara variables needed we construct our RNN as follows :
W = at.matrix()
W_in_1 = at.matrix()
W_in_2 = at.matrix()
W_feedback = at.matrix()
W_out = at.matrix()
u = at.matrix() # it is a sequence of vectors
x0 = at.matrix() # initial state of x has to be a matrix, since
# it has to cover x[-3]
y0 = at.vector() # y0 is just a vector since scan has only to provide
# y[-1]
([x_vals, y_vals], updates) = aesara.scan(fn=oneStep,
sequences=dict(input=u, taps=[-4,-0]),
outputs_info=[dict(initial=x0, taps=[-3,-1]), y0],
non_sequences=[W, W_in_1, W_in_2, W_feedback, W_out],
strict=True)
# for second input y, scan adds -1 in output_taps by default
Now x_vals and y_vals are symbolic variables pointing to the
sequence of x and y values generated by iterating over u. The
sequence_taps, outputs_taps give to scan information about what
slices are exactly needed. Note that if we want to use x[t-k] we do
not need to also have x[t-(k-1)], x[t-(k-2)],.., but when applying
the compiled function, the numpy array given to represent this sequence
should be large enough to cover this values. Assume that we compile the
above function, and we give as u the array uvals = [0,1,2,3,4,5,6,7,8].
By abusing notations, scan will consider uvals[0] as u[-4], and
will start scanning from uvals[4] towards the end.
Conditional ending of Scan#
Scan can also be used as a repeat-until block. In such a case scan
will stop when either the maximal number of iteration is reached, or the
provided condition evaluates to True.
For an example, we will compute all powers of two smaller then some provided
value max_value.
def power_of_2(previous_power, max_value):
return previous_power*2, aesara.scan.utils.until(previous_power*2 > max_value)
max_value = at.scalar()
values, _ = aesara.scan(power_of_2,
outputs_info = at.constant(1.),
non_sequences = max_value,
n_steps = 1024)
f = aesara.function([max_value], values)
print(f(45))
[ 2. 4. 8. 16. 32. 64.]
As you can see, in order to terminate on condition, the only thing required
is that the inner function power_of_2 to return also the condition
wrapped in the class aesara.scan.utils.until. The condition has to be
expressed in terms of the arguments of the inner function (in this case
previous_power and max_value).
As a rule, scan always expects the condition to be the last thing returned by the inner function, otherwise an error will be raised.
Reducing Scan’s memory usage#
This section presents the scan_checkpoints function. In short, this
function reduces the memory usage of scan (at the cost of more computation
time) by not keeping in memory all the intermediate time steps of the loop,
and recomputing them when computing the gradients. This function is therefore
only useful if you need to compute the gradient of the output of scan with
respect to its inputs, and shouldn’t be used otherwise.
Before going more into the details, here are its current limitations:
It only works in the case where only the output of the last time step is needed, like when computing
A**kor in anencoder-decodersetup.It only accepts sequences of the same length.
If
n_stepsis specified, it has the same value as the length of any sequences.It is singly-recurrent, meaning that only the previous time step can be used to compute the current one (i.e.
h[t]can only depend onh[t-1]). In other words,tapscan not be used insequencesandoutputs_info.
Often, in order to be able to compute the gradients through scan operations,
Aesara needs to keep in memory some intermediate computations of scan. This
can sometimes use a prohibitively large amount of memory.
scan_checkpoints allows to discard some of those intermediate steps and
recompute them again when computing the gradients. Its save_every_N argument
specifies the number time steps to do without storing the intermediate results.
For example, save_every_N = 4 will reduce the memory usage by 4, while having
to recompute 3/4 time steps of the forward loop. Since the grad of scan is
about 6x slower than the forward, a ~20% slowdown is expected. Apart from the
save_every_N argument and the current limitations, the usage of this function
is similar to the classic scan function.
Improving Scan’s performance#
This section covers some ways to improve performance of an Aesara function using Scan.
Minimizing Scan usage#
Scan makes it possible to define simple and compact graphs that can do the same work as much larger and more complicated graphs. However, it comes with a significant overhead. As such, when performance is the objective, a good rule of thumb is to perform as much of the computation as possible outside of Scan. This may have the effect of increasing memory usage but can also reduce the overhead introduces by using Scan.
Explicitly passing inputs of the inner function to scan#
It is possible, inside of Scan, to use variables previously defined outside of
the Scan without explicitly passing them as inputs to the Scan. However, it is
often more efficient to explicitly pass them as non-sequence inputs instead.
Section Using shared variables - Gibbs sampling provides an explanation for this and
section Using shared variables - the strict flag describes the strict flag, a tool that Scan
provides to help ensure that the inputs to the function inside Scan have all
been provided as explicit inputs to the scan() function.
Deactivating garbage collecting in Scan#
Deactivating the garbage collection for Scan can allow it to reuse memory between executions instead of always having to allocate new memory. This can improve performance at the cost of increased memory usage. By default, Scan reuses memory between iterations of the same execution but frees the memory after the last iteration.
There are two ways to achieve this, using the Aesara flag
config.scan__allow_gc and setting it to False, or using the argument
allow_gc of the function aesara.scan() and set it to False (when a value
is not provided for this argument, the value of the flag
config.scan__allow_gc is used).
Graph Rewrites#
This one is simple but still worth pointing out. Aesara is able to automatically recognize and rewrite many computation patterns. However, there are patterns that Aesara doesn’t rewrite because doing so would change the user interface (such as merging shared variables together into a single one, for instance). Additionally, Aesara doesn’t catch every case that it could rewrite and so it remains useful for performance that the user defines an efficient graph in the first place. This is also the case, and sometimes even more so, for the graph inside of Scan. This is because it will be executed many times for every execution of the Aesara function that contains it.
The LSTM tutorial on
DeepLearning.net provides an example of a
rewrite that Aesara cannot perform. Instead of performing many matrix
multiplications between matrix 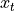 and each of the shared matrices
and each of the shared matrices
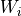 ,
, 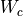 ,
, 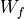 and
and 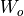 , the matrices
, the matrices
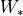 , are merged into a single shared matrix
, are merged into a single shared matrix 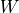 and the graph
performs a single larger matrix multiplication between
and the graph
performs a single larger matrix multiplication between 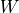 and
and
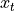 . The resulting matrix is then sliced to obtain the results of that
the small individual matrix multiplications would have produced. This
rewrite replaces several small and inefficient matrix multiplications by
a single larger one and thus improves performance at the cost of a potentially
higher memory usage.
. The resulting matrix is then sliced to obtain the results of that
the small individual matrix multiplications would have produced. This
rewrite replaces several small and inefficient matrix multiplications by
a single larger one and thus improves performance at the cost of a potentially
higher memory usage.
