Gradients API#
Symbolic gradient is usually computed from gradient.grad(), which offers a
more convenient syntax for the common case of wanting the gradient of some
scalar cost with respect to some input expressions. The grad_sources_inputs()
function does the underlying work, and is more flexible, but is also more
awkward to use when gradient.grad() can do the job.
Gradient related functions#
Driver for gradient calculations.
- class aesara.gradient.ConsiderConstant[source]#
- grad(args, g_outs)[source]#
Construct a graph for the gradient with respect to each input variable.
Each returned
Variablerepresents the gradient with respect to that input computed based on the symbolic gradients with respect to each output. If the output is not differentiable with respect to an input, then this method should return an instance of typeNullTypefor that input.Using the reverse-mode AD characterization given in [1]_, for a
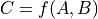 representing the function implemented by the
representing the function implemented by the Opand its two arguments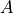 and
and 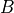 , given by the
, given by the
Variables ininputs, the values returned byOp.gradrepresent the quantities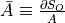 and
and
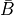 , for some scalar output term
, for some scalar output term 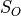 of
of 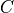 in
in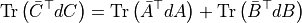
- Parameters:
inputs – The input variables.
output_grads – The gradients of the output variables.
- Returns:
grads – The gradients with respect to each
Variableininputs... [1] Giles, Mike. 2008. “An Extended Collection of Matrix Derivative Results for Forward and Reverse Mode Automatic Differentiation.”
- class aesara.gradient.DisconnectedGrad[source]#
- R_op(inputs, eval_points)[source]#
Construct a graph for the R-operator.
This method is primarily used by
Rop.- Parameters:
inputs – The
Opinputs.eval_points – A
Variableor list ofVariables with the same length as inputs. Each element ofeval_pointsspecifies the value of the corresponding input at the point where the R-operator is to be evaluated.
- Return type:
rval[i]should beRop(f=f_i(inputs), wrt=inputs, eval_points=eval_points).
- grad(args, g_outs)[source]#
Construct a graph for the gradient with respect to each input variable.
Each returned
Variablerepresents the gradient with respect to that input computed based on the symbolic gradients with respect to each output. If the output is not differentiable with respect to an input, then this method should return an instance of typeNullTypefor that input.Using the reverse-mode AD characterization given in [1]_, for a
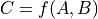 representing the function implemented by the
representing the function implemented by the Opand its two arguments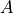 and
and 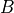 , given by the
, given by the
Variables ininputs, the values returned byOp.gradrepresent the quantities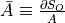 and
and
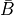 , for some scalar output term
, for some scalar output term 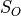 of
of 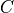 in
in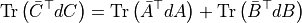
- Parameters:
inputs – The input variables.
output_grads – The gradients of the output variables.
- Returns:
grads – The gradients with respect to each
Variableininputs... [1] Giles, Mike. 2008. “An Extended Collection of Matrix Derivative Results for Forward and Reverse Mode Automatic Differentiation.”
- exception aesara.gradient.DisconnectedInputError[source]#
Raised when grad is asked to compute the gradient with respect to a disconnected input and disconnected_inputs=’raise’.
- class aesara.gradient.DisconnectedType[source]#
A type indicating that a variable is the result of taking the gradient of
cwith respect toxwhencis not a function ofx.It serves as a symbolic placeholder for
0, but conveys the extra information that this gradient is0because it is disconnected.- filter(data, strict=False, allow_downcast=None)[source]#
Return data or an appropriately wrapped/converted data.
Subclass implementations should raise a TypeError exception if the data is not of an acceptable type.
- Parameters:
data (array-like) – The data to be filtered/converted.
strict (bool (optional)) – If
True, the data returned must be the same as the data passed as an argument.allow_downcast (bool (optional)) – If
strictisFalse, andallow_downcastisTrue, the data may be cast to an appropriate type. Ifallow_downcastisFalse, it may only be up-cast and not lose precision. Ifallow_downcastisNone(default), the behaviour can be type-dependent, but for now it means only Python floats can be down-casted, and only to floatX scalars.
- class aesara.gradient.GradClip(clip_lower_bound, clip_upper_bound)[source]#
- grad(args, g_outs)[source]#
Construct a graph for the gradient with respect to each input variable.
Each returned
Variablerepresents the gradient with respect to that input computed based on the symbolic gradients with respect to each output. If the output is not differentiable with respect to an input, then this method should return an instance of typeNullTypefor that input.Using the reverse-mode AD characterization given in [1]_, for a
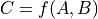 representing the function implemented by the
representing the function implemented by the Opand its two arguments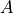 and
and 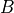 , given by the
, given by the
Variables ininputs, the values returned byOp.gradrepresent the quantities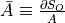 and
and
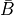 , for some scalar output term
, for some scalar output term 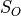 of
of 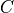 in
in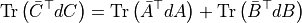
- Parameters:
inputs – The input variables.
output_grads – The gradients of the output variables.
- Returns:
grads – The gradients with respect to each
Variableininputs... [1] Giles, Mike. 2008. “An Extended Collection of Matrix Derivative Results for Forward and Reverse Mode Automatic Differentiation.”
- class aesara.gradient.GradScale(multiplier)[source]#
- grad(args, g_outs)[source]#
Construct a graph for the gradient with respect to each input variable.
Each returned
Variablerepresents the gradient with respect to that input computed based on the symbolic gradients with respect to each output. If the output is not differentiable with respect to an input, then this method should return an instance of typeNullTypefor that input.Using the reverse-mode AD characterization given in [1]_, for a
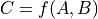 representing the function implemented by the
representing the function implemented by the Opand its two arguments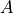 and
and 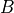 , given by the
, given by the
Variables ininputs, the values returned byOp.gradrepresent the quantities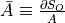 and
and
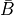 , for some scalar output term
, for some scalar output term 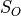 of
of 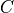 in
in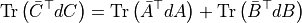
- Parameters:
inputs – The input variables.
output_grads – The gradients of the output variables.
- Returns:
grads – The gradients with respect to each
Variableininputs... [1] Giles, Mike. 2008. “An Extended Collection of Matrix Derivative Results for Forward and Reverse Mode Automatic Differentiation.”
- exception aesara.gradient.GradientError(arg, err_pos, shape, val1, val2, abs_err, rel_err, abs_tol, rel_tol)[source]#
This error is raised when a gradient is incorrectly calculated.
- aesara.gradient.Lop(f: Variable | Sequence[Variable], wrt: Variable | Sequence[Variable], eval_points: Variable | Sequence[Variable], consider_constant: Sequence[Variable] | None = None, disconnected_inputs: Literal['ignore', 'warn', 'raise'] = 'raise') Variable | None | Sequence[Variable | None][source]#
Computes the L-operator applied to
fwith respect towrtateval_points.Mathematically this stands for the Jacobian of
fwith respect towrtleft muliplied by theeval_points.- Parameters:
- Returns:
A symbolic expression satisfying
L_op[i] = sum_i (d f[i] / d wrt[j]) eval_point[i]where the indices in that expression are magic multidimensional
indices that specify both the position within a list and all
coordinates of the tensor elements.
If
fis a list/tuple, then return a list/tuple with the results.
- aesara.gradient.Rop(f: Variable | Sequence[Variable], wrt: Variable | Sequence[Variable], eval_points: Variable | Sequence[Variable], disconnected_outputs: Literal['ignore', 'warn', 'raise'] = 'raise', return_disconnected: Literal['none', 'zero', 'disconnected'] = 'zero') Variable | None | Sequence[Variable | None][source]#
Computes the R-operator applied to
fwith respect towrtateval_points.Mathematically this stands for the Jacobian of
fright multiplied by theeval_points.- Parameters:
f – The outputs of the computational graph to which the R-operator is applied.
wrt – Variables for which the R-operator of
fis computed.eval_points – Points at which to evaluate each of the variables in
wrt.disconnected_outputs –
Defines the behaviour if some of the variables in
fhave no dependency on any of the variable inwrt(or if all links are non-differentiable). The possible values are:'ignore': considers that the gradient on these parameters is zero.'warn': consider the gradient zero, and print a warning.'raise': raiseDisconnectedInputError.
return_disconnected –
'zero': Ifwrt[i]is disconnected, return valueiwill bewrt[i].zeros_like().'none': Ifwrt[i]is disconnected, return valueiwill beNone'disconnected': returns variables of typeDisconnectedType
- Returns:
A symbolic expression such obeying
R_op[i] = sum_j (d f[i] / d wrt[j]) eval_point[j],where the indices in that expression are magic multidimensional
indices that specify both the position within a list and all
coordinates of the tensor elements.
If
wrtis a list/tuple, then return a list/tuple with the results.
- class aesara.gradient.UndefinedGrad[source]#
- R_op(inputs, eval_points)[source]#
Construct a graph for the R-operator.
This method is primarily used by
Rop.- Parameters:
inputs – The
Opinputs.eval_points – A
Variableor list ofVariables with the same length as inputs. Each element ofeval_pointsspecifies the value of the corresponding input at the point where the R-operator is to be evaluated.
- Return type:
rval[i]should beRop(f=f_i(inputs), wrt=inputs, eval_points=eval_points).
- grad(args, g_outs)[source]#
Construct a graph for the gradient with respect to each input variable.
Each returned
Variablerepresents the gradient with respect to that input computed based on the symbolic gradients with respect to each output. If the output is not differentiable with respect to an input, then this method should return an instance of typeNullTypefor that input.Using the reverse-mode AD characterization given in [1]_, for a
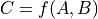 representing the function implemented by the
representing the function implemented by the Opand its two arguments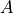 and
and 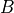 , given by the
, given by the
Variables ininputs, the values returned byOp.gradrepresent the quantities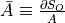 and
and
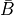 , for some scalar output term
, for some scalar output term 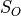 of
of 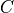 in
in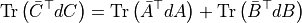
- Parameters:
inputs – The input variables.
output_grads – The gradients of the output variables.
- Returns:
grads – The gradients with respect to each
Variableininputs... [1] Giles, Mike. 2008. “An Extended Collection of Matrix Derivative Results for Forward and Reverse Mode Automatic Differentiation.”
- class aesara.gradient.ZeroGrad[source]#
- R_op(inputs, eval_points)[source]#
Construct a graph for the R-operator.
This method is primarily used by
Rop.- Parameters:
inputs – The
Opinputs.eval_points – A
Variableor list ofVariables with the same length as inputs. Each element ofeval_pointsspecifies the value of the corresponding input at the point where the R-operator is to be evaluated.
- Return type:
rval[i]should beRop(f=f_i(inputs), wrt=inputs, eval_points=eval_points).
- grad(args, g_outs)[source]#
Construct a graph for the gradient with respect to each input variable.
Each returned
Variablerepresents the gradient with respect to that input computed based on the symbolic gradients with respect to each output. If the output is not differentiable with respect to an input, then this method should return an instance of typeNullTypefor that input.Using the reverse-mode AD characterization given in [1]_, for a
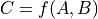 representing the function implemented by the
representing the function implemented by the Opand its two arguments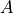 and
and 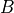 , given by the
, given by the
Variables ininputs, the values returned byOp.gradrepresent the quantities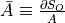 and
and
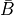 , for some scalar output term
, for some scalar output term 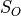 of
of 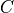 in
in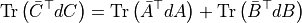
- Parameters:
inputs – The input variables.
output_grads – The gradients of the output variables.
- Returns:
grads – The gradients with respect to each
Variableininputs... [1] Giles, Mike. 2008. “An Extended Collection of Matrix Derivative Results for Forward and Reverse Mode Automatic Differentiation.”
- aesara.gradient.as_list_or_tuple(use_list: bool, use_tuple: bool, outputs: V | Sequence[V]) V | List[V] | Tuple[V, ...][source]#
Return either a single object or a list/tuple of objects.
If
use_listis True,outputsis returned as a list (ifoutputsis not a list or a tuple then it is converted in a one element list). Ifuse_tupleis True,outputsis returned as a tuple (ifoutputsis not a list or a tuple then it is converted into a one element tuple). Otherwise (if both flags are false),outputsis returned.
- aesara.gradient.consider_constant(x)[source]#
Consider an expression constant when computing gradients.
DEPRECATED: use
zero_gradordisconnected_gradinstead.The expression itself is unaffected, but when its gradient is computed, or the gradient of another expression that this expression is a subexpression of, it will not be backpropagated through. In other words, the gradient of the expression is truncated to 0.
- Parameters:
x – A Aesara expression whose gradient should be truncated.
- Returns:
The expression is returned unmodified, but its gradient is now truncated to 0.
New in version 0.7.
- aesara.gradient.disconnected_grad(x)[source]#
Consider an expression constant when computing gradients.
It will effectively not backpropagating through it.
The expression itself is unaffected, but when its gradient is computed, or the gradient of another expression that this expression is a subexpression of, it will not be backpropagated through. This is effectively equivalent to truncating the gradient expression to 0, but is executed faster than zero_grad(), which stilll has to go through the underlying computational graph related to the expression.
- aesara.gradient.grad(cost: Variable | None, wrt: Variable | Sequence[Variable], consider_constant: Sequence[Variable] | None = None, disconnected_inputs: Literal['ignore', 'warn', 'raise'] = 'raise', add_names: bool = True, known_grads: Mapping[Variable, Variable] | None = None, return_disconnected: Literal['none', 'zero', 'disconnected'] = 'zero', null_gradients: Literal['raise', 'return'] = 'raise') Variable | None | Sequence[Variable | None][source]#
Return symbolic gradients of one cost with respect to one or more variables.
For more information about how automatic differentiation works in Aesara, see
gradient. For information on how to implement the gradient of a certain Op, seegrad().- Parameters:
cost – Value that we are differentiating (i.e. for which we want the gradient). May be
Noneifknown_gradsis provided.wrt – The term(s) with respect to which we want gradients.
consider_constant – Expressions not to backpropagate through.
disconnected_inputs ({'ignore', 'warn', 'raise'}) –
Defines the behaviour if some of the variables in
wrtare not part of the computational graph computingcost(or if all links are non-differentiable). The possible values are:'ignore': considers that the gradient on these parameters is zero'warn': consider the gradient zero, and print a warning'raise': raiseDisconnectedInputError
add_names – If
True, variables generated bygradwill be named(d<cost.name>/d<wrt.name>)provided that bothcostandwrthave names.known_grads – An ordered dictionary mapping variables to their gradients. This is useful in the case where you know the gradients of some variables but do not know the original cost.
return_disconnected –
'zero': Ifwrt[i]is disconnected, return valueiwill bewrt[i].zeros_like()'none': Ifwrt[i]is disconnected, return valueiwill beNone'disconnected': returns variables of typeDisconnectedType
null_gradients –
Defines the behaviour when some of the variables in
wrthave a null gradient. The possibles values are:'raise': raise aNullTypeGradErrorexception'return': return the null gradients
- Returns:
A symbolic expression for the gradient of
costwith respect to eachof the
wrtterms. If an element ofwrtis not differentiable withrespect to the output, then a zero variable is returned.
- aesara.gradient.grad_clip(x, lower_bound, upper_bound)[source]#
This op do a view in the forward, but clip the gradient.
This is an elemwise operation.
- Parameters:
x – The variable we want its gradient inputs clipped
lower_bound – The lower bound of the gradient value
upper_bound – The upper bound of the gradient value.
Examples
>>> x = aesara.tensor.type.scalar() >>> z = aesara.gradient.grad(grad_clip(x, -1, 1)**2, x) >>> z2 = aesara.gradient.grad(x**2, x) >>> f = aesara.function([x], outputs = [z, z2]) >>> print(f(2.0)) [array(1.0), array(4.0)]
Notes
We register an opt in tensor/opt.py that remove the GradClip. So it have 0 cost in the forward and only do work in the grad.
- aesara.gradient.grad_not_implemented(op, x_pos, x, comment='')[source]#
Return an un-computable symbolic variable of type
x.type.If any call to
gradresults in an expression containing this un-computable variable, an exception (e.g.NotImplementedError) will be raised indicating that the gradient on thex_pos’th input ofophas not been implemented. Likewise if any call to aesara.function involves this variable.Optionally adds a comment to the exception explaining why this gradient is not implemented.
- aesara.gradient.grad_scale(x, multiplier)[source]#
This op scale or inverse the gradient in the backpropagation.
- Parameters:
x – The variable we want its gradient inputs scale
multiplier – Scale of the gradient
Examples
>>> x = aesara.tensor.fscalar() >>> fx = aesara.tensor.sin(x) >>> fp = aesara.grad(fx, wrt=x) >>> fprime = aesara.function([x], fp) >>> print(fprime(2)) -0.416... >>> f_inverse=grad_scale(fx, -1.) >>> fpp = aesara.grad(f_inverse, wrt=x) >>> fpprime = aesara.function([x], fpp) >>> print(fpprime(2)) 0.416...
- aesara.gradient.grad_undefined(op, x_pos, x, comment='')[source]#
Return an un-computable symbolic variable of type
x.type.If any call to
gradresults in an expression containing this un-computable variable, an exception (e.g.GradUndefinedError) will be raised indicating that the gradient on thex_pos’th input ofopis mathematically undefined. Likewise if any call to aesara.function involves this variable.Optionally adds a comment to the exception explaining why this gradient is not defined.
- aesara.gradient.hessian(cost, wrt, consider_constant=None, disconnected_inputs='raise')[source]#
- Parameters:
cost (Scalar (0-dimensional) variable.) –
wrt (Vector (1-dimensional tensor) 'Variable' or list of) –
Variables (vectors (1-dimensional tensors)) –
consider_constant – a list of expressions not to backpropagate through
disconnected_inputs (string) –
Defines the behaviour if some of the variables in
wrtare not part of the computational graph computingcost(or if all links are non-differentiable). The possible values are:’ignore’: considers that the gradient on these parameters is zero.
’warn’: consider the gradient zero, and print a warning.
’raise’: raise an exception.
- Returns:
The Hessian of the
costwith respect to (elements of)wrt. If an element ofwrtis not differentiable with respect to the output, then a zero variable is returned. The return value is of same type aswrt: a list/tuple or TensorVariable in all cases.- Return type:
Variableor list/tuple of Variables
- aesara.gradient.jacobian(expression, wrt, consider_constant=None, disconnected_inputs='raise')[source]#
Compute the full Jacobian, row by row.
- Parameters:
expression (Vector (1-dimensional)
Variable) – Values that we are differentiating (that we want the Jacobian of)wrt (
Variableor list of Variables) – Term[s] with respect to which we compute the Jacobianconsider_constant (list of variables) – Expressions not to backpropagate through
disconnected_inputs (string) –
Defines the behaviour if some of the variables in
wrtare not part of the computational graph computingcost(or if all links are non-differentiable). The possible values are:’ignore’: considers that the gradient on these parameters is zero.
’warn’: consider the gradient zero, and print a warning.
’raise’: raise an exception.
- Returns:
The Jacobian of
expressionwith respect to (elements of)wrt. If an element ofwrtis not differentiable with respect to the output, then a zero variable is returned. The return value is of same type aswrt: a list/tuple or TensorVariable in all cases.- Return type:
Variableor list/tuple of Variables (depending uponwrt)
- class aesara.gradient.numeric_grad(f, pt, eps=None, out_type=None)[source]#
Compute the numeric derivative of a scalar-valued function at a particular point.
- static abs_rel_err(a, b)[source]#
Return absolute and relative error between a and b.
The relative error is a small number when a and b are close, relative to how big they are.
- Formulas used:
abs_err = abs(a - b)
rel_err = abs_err / max(abs(a) + abs(b), 1e-8)
The denominator is clipped at 1e-8 to avoid dividing by 0 when a and b are both close to 0.
The tuple (abs_err, rel_err) is returned
- abs_rel_errors(g_pt)[source]#
Return the abs and rel error of gradient estimate
g_ptg_ptmust be a list of ndarrays of the same length as self.gf, otherwise a ValueError is raised.Corresponding ndarrays in
g_ptandself.gfmust have the same shape or ValueError is raised.
- max_err(g_pt, abs_tol, rel_tol)[source]#
Find the biggest error between g_pt and self.gf.
What is measured is the violation of relative and absolute errors, wrt the provided tolerances (abs_tol, rel_tol). A value > 1 means both tolerances are exceeded.
Return the argmax of min(abs_err / abs_tol, rel_err / rel_tol) over g_pt, as well as abs_err and rel_err at this point.
- aesara.gradient.subgraph_grad(wrt, end, start=None, cost=None, details=False)[source]#
With respect to
wrt, computes gradients of cost and/or from existingstartgradients, up to theendvariables of a symbolic digraph. In other words, computes gradients for a subgraph of the symbolic aesara function. Ignores all disconnected inputs.This can be useful when one needs to perform the gradient descent iteratively (e.g. one layer at a time in an MLP), or when a particular operation is not differentiable in aesara (e.g. stochastic sampling from a multinomial). In the latter case, the gradient of the non-differentiable process could be approximated by user-defined formula, which could be calculated using the gradients of a cost with respect to samples (0s and 1s). These gradients are obtained by performing a subgraph_grad from the
costor previously known gradients (start) up to the outputs of the stochastic process (end). A dictionary mapping gradients obtained from the user-defined differentiation of the process, to variables, could then be fed into another subgraph_grad asstartwith any othercost(e.g. weight decay).In an MLP, we could use subgraph_grad to iteratively backpropagate:
x, t = aesara.tensor.fvector('x'), aesara.tensor.fvector('t') w1 = aesara.shared(np.random.standard_normal((3,4))) w2 = aesara.shared(np.random.standard_normal((4,2))) a1 = aesara.tensor.tanh(aesara.tensor.dot(x,w1)) a2 = aesara.tensor.tanh(aesara.tensor.dot(a1,w2)) cost2 = aesara.tensor.square(a2 - t).sum() cost2 += aesara.tensor.square(w2.sum()) cost1 = aesara.tensor.square(w1.sum()) params = [[w2],[w1]] costs = [cost2,cost1] grad_ends = [[a1], [x]] next_grad = None param_grads = [] for i in range(2): param_grad, next_grad = aesara.subgraph_grad( wrt=params[i], end=grad_ends[i], start=next_grad, cost=costs[i] ) next_grad = dict(zip(grad_ends[i], next_grad)) param_grads.extend(param_grad)
- Parameters:
wrt (list of variables) – Gradients are computed with respect to
wrt.end (list of variables) – Aesara variables at which to end gradient descent (they are considered constant in aesara.grad). For convenience, the gradients with respect to these variables are also returned.
start (dictionary of variables) – If not None, a dictionary mapping variables to their gradients. This is useful when the gradient on some variables are known. These are used to compute the gradients backwards up to the variables in
end(they are used as known_grad in aesara.grad).cost (
Variablescalar (0-dimensional) variable) –Additional costs for which to compute the gradients. For example, these could be weight decay, an l1 constraint, MSE, NLL, etc. May optionally be None if start is provided.
Warning
If the gradients of
costwith respect to any of thestartvariables is already part of thestartdictionary, then it may be counted twice with respect towrtandend.details (bool) – When True, additionally returns the list of gradients from
startand ofcost, respectively, with respect towrt(notend).
- Returns:
Returns lists of gradients with respect to
wrtandend, respectively.- Return type:
Tuple of 2 or 4 Lists of Variables
New in version 0.7.
- aesara.gradient.undefined_grad(x)[source]#
Consider the gradient of this variable undefined.
This will generate an error message if its gradient is taken.
The expression itself is unaffected, but when its gradient is computed, or the gradient of another expression that this expression is a subexpression of, an error message will be generated specifying such gradient is not defined.
- aesara.gradient.verify_grad(fun: Callable, pt: List[ndarray], n_tests: int = 2, rng: Generator | RandomState | None = None, eps: float | None = None, out_type: str | None = None, abs_tol: float | None = None, rel_tol: float | None = None, mode: Mode | str | None = None, cast_to_output_type: bool = False, no_debug_ref: bool = True)[source]#
Test a gradient by Finite Difference Method. Raise error on failure.
Raises an Exception if the difference between the analytic gradient and numerical gradient (computed through the Finite Difference Method) of a random projection of the fun’s output to a scalar exceeds the given tolerance.
Examples
>>> verify_grad(aesara.tensor.tanh, ... (np.asarray([[2, 3, 4], [-1, 3.3, 9.9]]),), ... rng=np.random.default_rng(23098))
- Parameters:
fun –
funtakes Aesara variables as inputs, and returns an Aesara variable. For instance, anOpinstance with a single output.pt – Input values, points where the gradient is estimated. These arrays must be either float16, float32, or float64 arrays.
n_tests – Number o to run the test.
rng – Random number generator used to sample the output random projection
u, we test gradient ofsum(u * fun)atpt.eps – Step size used in the Finite Difference Method (Default
Noneis type-dependent). Raising the value ofepscan raise or lower the absolute and relative errors of the verification depending on theOp. Raisingepsdoes not lower the verification quality for linear operations. It is better to raiseepsthan raisingabs_tolorrel_tol.out_type – Dtype of output, if complex (i.e.,
'complex32'or'complex64')abs_tol – Absolute tolerance used as threshold for gradient comparison
rel_tol – Relative tolerance used as threshold for gradient comparison
cast_to_output_type – If the output is float32 and
cast_to_output_typeisTrue, cast the random projection to float32; otherwise, it is float64. float16 is not handled here.no_debug_ref – Don’t use
DebugModefor the numerical gradient function.
Notes
This function does not support multiple outputs. In
tests.scan.test_basicthere is an experimentalverify_gradthat covers that case as well by using random projections.
- aesara.gradient.zero_grad(x)[source]#
Consider an expression constant when computing gradients.
The expression itself is unaffected, but when its gradient is computed, or the gradient of another expression that this expression is a subexpression of, it will be backpropagated through with a value of zero. In other words, the gradient of the expression is truncated to 0.
List of Implemented R op#
See the gradient tutorial for the R op documentation.
- list of ops that support R-op:
- with test
SpecifyShape
MaxAndArgmax
Subtensor
IncSubtensor set_subtensor too
Alloc
Dot
Elemwise
Sum
Softmax
Shape
Join
Rebroadcast
Reshape
DimShuffle
Scan [In tests/scan/test_basic.test_rop]
- without test
Split
ARange
ScalarFromTensor
AdvancedSubtensor1
AdvancedIncSubtensor1
AdvancedIncSubtensor
Partial list of ops without support for R-op:
All sparse ops
All linear algebra ops.
PermuteRowElements
AdvancedSubtensor
TensorDot
Outer
Prod
MulwithoutZeros
ProdWithoutZeros
CAReduce(for max,… done for MaxAndArgmax op)
MaxAndArgmax(only for matrix on axis 0 or 1)
