graph – Objects and functions for computational graphs

class aesara.graph.op.HasInnerGraph

A mixin for an Op that contain an inner graph.

abstract clone() → Op

Clone the Op and its inner-graph.

fgraph: FunctionGraph

A FunctionGraph of the inner function.

abstract property fn: Function

The compiled inner-graph function.

abstract property inner_inputs: List[Variable]

The inner function’s inputs.

abstract property inner_outputs: List[Variable]

The inner function’s outputs.

class aesara.graph.op.Op

A class that models and constructs operations in a graph.

A Op instance has several responsibilities:

• construct Apply nodes via Op.make_node() method,

• perform the numeric calculation of the modeled operation via the Op.perform() method,

• and (optionally) build the gradient-calculating sub-graphs via the Op.grad() method.

To see how Op, Type, Variable, and Apply fit together see the page on graph – Interface for the Aesara graph.

For more details regarding how these methods should behave: see the Op Contract in the sphinx docs (advanced tutorial on Op making).

L_op(inputs: Sequence[Variable], outputs: Sequence[Variable], output_grads: Sequence[Variable]) → List[Variable]

Construct a graph for the L-operator.

The L-operator computes a row vector times the Jacobian.

This method dispatches to Op.grad() by default. In one sense, this method provides the original outputs when they’re needed to compute the return value, whereas Op.grad doesn’t.

See Op.grad for a mathematical explanation of the inputs and outputs of this method.

Parameters:

• inputs – The inputs of the Apply node using this Op.

• outputs – The outputs of the Apply node using this Op

• output_grads – The gradients with respect to each Variable in inputs.

R_op(inputs: List[Variable], eval_points: Variable | List[Variable]) → List[Variable]

Construct a graph for the R-operator.

This method is primarily used by Rop.

Parameters:

• inputs – The Op inputs.

• eval_points – A Variable or list of Variables with the same length as inputs. Each element of eval_points specifies the value of the corresponding input at the point where the R-operator is to be evaluated.

Return type:

rval[i] should be Rop(f=f_i(inputs), wrt=inputs, eval_points=eval_points).

static add_tag_trace(thing: T, user_line: int | None = None) → T

Add tag.trace to a node or variable.

The argument is returned after being affected (inplace).

Parameters:

• thing – The object where we add .tag.trace.

• user_line – The max number of user line to keep.

Notes

We also use config.traceback__limit for the maximum number of stack level we look.

default_output: int | None = None

An int that specifies which output Op.__call__() should return. If None, then all outputs are returned.

A subclass should not change this class variable, but instead override it with a subclass variable or an instance variable.

destroy_map: Dict[int, List[int]] = {}

A dict that maps output indices to the input indices upon which they operate in-place.

Examples

destroy_map = {0: [1]} # first output operates in-place on second input
destroy_map = {1: [0]} # second output operates in-place on first input

do_constant_folding(fgraph: FunctionGraph, node: Apply) → bool

Determine whether or not constant folding should be performed for the given node.

This allows each Op to determine if it wants to be constant folded when all its inputs are constant. This allows it to choose where it puts its memory/speed trade-off. Also, it could make things faster as constants can’t be used for in-place operations (see *IncSubtensor).

Parameters:

node (Apply) – The node for which the constant folding determination is made.

Returns:

res

Return type:

bool

get_params(node: Apply) → Params

Try to get parameters for the Op when Op.params_type is set to a ParamsType.

grad(inputs: Sequence[Variable], output_grads: Sequence[Variable]) → List[Variable]

Construct a graph for the gradient with respect to each input variable.

Each returned Variable represents the gradient with respect to that input computed based on the symbolic gradients with respect to each output. If the output is not differentiable with respect to an input, then this method should return an instance of type NullType for that input.

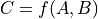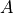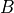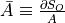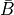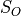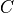Using the reverse-mode AD characterization given in [1]_, for a representing the function implemented by the Op and its two arguments and , given by the Variables in inputs, the values returned by Op.grad represent the quantities and , for some scalar output term of in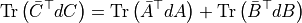

Parameters:

• inputs – The input variables.

• output_grads – The gradients of the output variables.

Returns:

• grads – The gradients with respect to each Variable in inputs.

• .. [1] Giles, Mike. 2008. “An Extended Collection of Matrix Derivative Results for Forward and Reverse Mode Automatic Differentiation.”

make_node(*inputs: Variable) → Apply

Construct an Apply node that represent the application of this operation to the given inputs.

This must be implemented by sub-classes.

Returns:

node – The constructed Apply node.

Return type:

Apply

make_py_thunk(node: Apply, storage_map: Dict[Variable, List[Any | None]], compute_map: Dict[Variable, List[bool]], no_recycling: List[Variable], debug: bool = False) → ThunkType

Make a Python thunk.

Like Op.make_thunk() but only makes Python thunks.

make_thunk(node: Apply, storage_map: Dict[Variable, List[Any | None]], compute_map: Dict[Variable, List[bool]], no_recycling: List[Variable], impl: str | None = None) → ThunkType

Create a thunk.

This function must return a thunk, that is a zero-arguments function that encapsulates the computation to be performed by this op on the arguments of the node.

Parameters:

• node – Something previously returned by Op.make_node().

• storage_map – A dict mapping Variables to single-element lists where a computed value for each Variable may be found.

• compute_map – A dict mapping Variables to single-element lists where a boolean value can be found. The boolean indicates whether the Variable’s storage_map container contains a valid value (i.e. True) or whether it has not been computed yet (i.e. False).

• no_recycling – List of Variables for which it is forbidden to reuse memory allocated by a previous call.

• impl (str) – Description for the type of node created (e.g. "c", "py", etc.)

Notes

If the thunk consults the storage_map on every call, it is safe for it to ignore the no_recycling argument, because elements of the no_recycling list will have a value of None in the storage_map. If the thunk can potentially cache return values (like CLinker does), then it must not do so for variables in the no_recycling list.

Op.prepare_node() is always called. If it tries 'c' and it fails, then it tries 'py', and Op.prepare_node() will be called twice.

abstract perform(node: Apply, inputs: Sequence[Any], output_storage: List[List[Any | None]], params: Tuple[Any] | None = None) → None

Calculate the function on the inputs and put the variables in the output storage.

Parameters:

• node – The symbolic Apply node that represents this computation.

• inputs – Immutable sequence of non-symbolic/numeric inputs. These are the values of each Variable in node.inputs.

• output_storage – List of mutable single-element lists (do not change the length of these lists). Each sub-list corresponds to value of each Variable in node.outputs. The primary purpose of this method is to set the values of these sub-lists.

• params – A tuple containing the values of each entry in Op.__props__.

Notes

The output_storage list might contain data. If an element of output_storage is not None, it has to be of the right type, for instance, for a TensorVariable, it has to be a NumPy ndarray with the right number of dimensions and the correct dtype. Its shape and stride pattern can be arbitrary. It is not guaranteed that such pre-set values were produced by a previous call to this Op.perform(); they could’ve been allocated by another Op’s perform method. An Op is free to reuse output_storage as it sees fit, or to discard it and allocate new memory.

prepare_node(node: Apply, storage_map: Dict[Variable, List[Any | None]] | None, compute_map: Dict[Variable, List[bool]] | None, impl: str | None) → None

Make any special modifications that the Op needs before doing Op.make_thunk().

This can modify the node inplace and should return nothing.

It can be called multiple time with different impl values.

Warning

It is the Op’s responsibility to not re-prepare the node when it isn’t good to do so.

view_map: Dict[int, List[int]] = {}

A dict that maps output indices to the input indices of which they are a view.

Examples

view_map = {0: [1]} # first output is a view of second input
view_map = {1: [0]} # second output is a view of first input

class aesara.graph.op.ThunkType(*args, **kwargs)

aesara.graph.op.compute_test_value(node: Apply)

Computes the test value of a node.

Parameters:

node (Apply) – The Apply node for which the test value is computed.

Returns:

The tag.test_values are updated in each Variable in node.outputs.

Return type:

None

aesara.graph.op.get_test_value(v: Any) → Any

Get the test value for v.

If input v is not already a variable, it is turned into one by calling as_tensor_variable(v).

Raises:

AttributeError` if no test value is set –

aesara.graph.op.get_test_values(*args: Variable) → Any | List[Any]

Get test values for multiple Variables.

Intended use:

for val_1, ..., val_n in get_debug_values(var_1, ..., var_n):
    if some condition on val_1, ..., val_n is not met:
        missing_test_message("condition was not met")

Given a list of variables, get_debug_values does one of three things:

1. If the interactive debugger is off, returns an empty list

2. If the interactive debugger is on, and all variables have debug values, returns a list containing a single element. This single element is either:

   1. if there is only one variable, the element is its

      value

   2. otherwise, a tuple containing debug values of all

      the variables.

3. If the interactive debugger is on, and some variable does not have a debug value, issue a missing_test_message about the variable, and, if still in control of execution, return an empty list.

aesara.graph.op.missing_test_message(msg: str) → None

Display a message saying that some test_value is missing.

This uses the appropriate form based on config.compute_test_value:

off:

The interactive debugger is off, so we do nothing.

ignore:

The interactive debugger is set to ignore missing inputs, so do nothing.

warn:

Display msg as a warning.

Raises:

AttributeError – With msg as the exception text.