sparse.sandbox – Sparse Op Sandbox#
API#
Convolution-like operations with sparse matrix multiplication.
To read about different sparse formats, see U{http://www-users.cs.umn.edu/~saad/software/SPARSKIT/paper.ps}.
@todo: Automatic methods for determining best sparse format?
- class aesara.sparse.sandbox.sp.ConvolutionIndices[source]#
Build indices for a sparse CSC matrix that could implement A (convolve) B.
This generates a sparse matrix M, which generates a stack of image patches when computing the dot product of M with image patch. Convolution is then simply the dot product of (img x M) and the kernels.
- static evaluate(inshp, kshp, strides=(1, 1), nkern=1, mode='valid', ws=True)[source]#
Build a sparse matrix which can be used for performing… * convolution: in this case, the dot product of this matrix with the input images will generate a stack of images patches. Convolution is then a tensordot operation of the filters and the patch stack. * sparse local connections: in this case, the sparse matrix allows us to operate the weight matrix as if it were fully-connected. The structured-dot with the input image gives the output for the following layer.
- Parameters:
ker_shape – shape of kernel to apply (smaller than image)
img_shape – shape of input images
mode – ‘valid’ generates output only when kernel and image overlap overlap fully. Convolution obtained by zero-padding the input
ws – must be always True
(dx,dy) – offset parameter. In the case of no weight sharing, gives the pixel offset between two receptive fields. With weight sharing gives the offset between the top-left pixels of the generated patches
- Return type:
tuple(indices, indptr, logical_shape, sp_type, out_img_shp)
- Returns:
the structure of a sparse matrix, and the logical dimensions of the image which will be the result of filtering.
- perform(node, inputs, outputs)[source]#
Calculate the function on the inputs and put the variables in the output storage.
- Parameters:
node – The symbolic
Applynode that represents this computation.inputs – Immutable sequence of non-symbolic/numeric inputs. These are the values of each
Variableinnode.inputs.output_storage – List of mutable single-element lists (do not change the length of these lists). Each sub-list corresponds to value of each
Variableinnode.outputs. The primary purpose of this method is to set the values of these sub-lists.params – A tuple containing the values of each entry in
Op.__props__.
Notes
The
output_storagelist might contain data. If an element of output_storage is notNone, it has to be of the right type, for instance, for aTensorVariable, it has to be a NumPyndarraywith the right number of dimensions and the correct dtype. Its shape and stride pattern can be arbitrary. It is not guaranteed that such pre-set values were produced by a previous call to thisOp.perform(); they could’ve been allocated by anotherOp’sperformmethod. AnOpis free to reuseoutput_storageas it sees fit, or to discard it and allocate new memory.
- aesara.sparse.sandbox.sp.convolve(kerns, kshp, nkern, images, imgshp, step=(1, 1), bias=None, mode='valid', flatten=True)[source]#
Convolution implementation by sparse matrix multiplication.
- Note:
For best speed, put the matrix which you expect to be smaller as the ‘kernel’ argument
“images” is assumed to be a matrix of shape batch_size x img_size, where the second dimension represents each image in raster order
If flatten is “False”, the output feature map will have shape:
batch_size x number of kernels x output_size
If flatten is “True”, the output feature map will have shape:
batch_size x number of kernels * output_size
Note
IMPORTANT: note that this means that each feature map (image generate by each kernel) is contiguous in memory. The memory layout will therefore be: [ <feature_map_0> <feature_map_1> … <feature_map_n>], where <feature_map> represents a “feature map” in raster order
kerns is a 2D tensor of shape nkern x N.prod(kshp)
- Parameters:
kerns – 2D tensor containing kernels which are applied at every pixel
kshp – tuple containing actual dimensions of kernel (not symbolic)
nkern – number of kernels/filters to apply. nkern=1 will apply one common filter to all input pixels
images – tensor containing images on which to apply convolution
imgshp – tuple containing image dimensions
step – determines number of pixels between adjacent receptive fields (tuple containing dx,dy values)
mode – ‘full’, ‘valid’ see CSM.evaluate function for details
sumdims – dimensions over which to sum for the tensordot operation. By default ((2,),(1,)) assumes kerns is a nkern x kernsize matrix and images is a batchsize x imgsize matrix containing flattened images in raster order
flatten – flatten the last 2 dimensions of the output. By default, instead of generating a batchsize x outsize x nkern tensor, will flatten to batchsize x outsize*nkern
- Returns:
out1, symbolic result
- Returns:
out2, logical shape of the output img (nkern,height,width)
- TODO:
test for 1D and think of how to do n-d convolutions
- aesara.sparse.sandbox.sp.max_pool(images, imgshp, maxpoolshp)[source]#
Implements a max pooling layer
Takes as input a 2D tensor of shape batch_size x img_size and performs max pooling. Max pooling downsamples by taking the max value in a given area, here defined by maxpoolshp. Outputs a 2D tensor of shape batch_size x output_size.
- Parameters:
images – 2D tensor containing images on which to apply convolution. Assumed to be of shape batch_size x img_size
imgshp – tuple containing image dimensions
maxpoolshp – tuple containing shape of area to max pool over
- Returns:
out1, symbolic result (2D tensor)
- Returns:
out2, logical shape of the output
- class aesara.sparse.sandbox.sp2.Binomial(format, dtype)[source]#
Return a sparse matrix having random values from a binomial density having number of experiment
nand probability of successp.WARNING: This Op is NOT deterministic, as calling it twice with the same inputs will NOT give the same result. This is a violation of Aesara’s contract for Ops
- Parameters:
n – Tensor scalar representing the number of experiment.
p – Tensor scalar representing the probability of success.
shape – Tensor vector for the output shape.
- Returns:
A sparse matrix of integers representing the number of success.
- grad(inputs, gout)[source]#
Construct a graph for the gradient with respect to each input variable.
Each returned
Variablerepresents the gradient with respect to that input computed based on the symbolic gradients with respect to each output. If the output is not differentiable with respect to an input, then this method should return an instance of typeNullTypefor that input.Using the reverse-mode AD characterization given in [1]_, for a
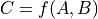 representing the function implemented by the
representing the function implemented by the Opand its two arguments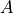 and
and 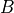 , given by the
, given by the
Variables ininputs, the values returned byOp.gradrepresent the quantities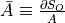 and
and
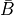 , for some scalar output term
, for some scalar output term 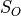 of
of 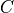 in
in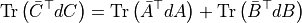
- Parameters:
inputs – The input variables.
output_grads – The gradients of the output variables.
- Returns:
grads – The gradients with respect to each
Variableininputs... [1] Giles, Mike. 2008. “An Extended Collection of Matrix Derivative Results for Forward and Reverse Mode Automatic Differentiation.”
- make_node(n, p, shape)[source]#
Construct an
Applynode that represent the application of this operation to the given inputs.This must be implemented by sub-classes.
- Returns:
node – The constructed
Applynode.- Return type:
- perform(node, inputs, outputs)[source]#
Calculate the function on the inputs and put the variables in the output storage.
- Parameters:
node – The symbolic
Applynode that represents this computation.inputs – Immutable sequence of non-symbolic/numeric inputs. These are the values of each
Variableinnode.inputs.output_storage – List of mutable single-element lists (do not change the length of these lists). Each sub-list corresponds to value of each
Variableinnode.outputs. The primary purpose of this method is to set the values of these sub-lists.params – A tuple containing the values of each entry in
Op.__props__.
Notes
The
output_storagelist might contain data. If an element of output_storage is notNone, it has to be of the right type, for instance, for aTensorVariable, it has to be a NumPyndarraywith the right number of dimensions and the correct dtype. Its shape and stride pattern can be arbitrary. It is not guaranteed that such pre-set values were produced by a previous call to thisOp.perform(); they could’ve been allocated by anotherOp’sperformmethod. AnOpis free to reuseoutput_storageas it sees fit, or to discard it and allocate new memory.
- class aesara.sparse.sandbox.sp2.Multinomial[source]#
Return a sparse matrix having random values from a multinomial density having number of experiment
nand probability of successp.WARNING: This Op is NOT deterministic, as calling it twice with the same inputs will NOT give the same result. This is a violation of Aesara’s contract for Ops
- Parameters:
n – Tensor type vector or scalar representing the number of experiment for each row. If
nis a scalar, it will be used for each row.p – Sparse matrix of probability where each row is a probability vector representing the probability of success. N.B. Each row must sum to one.
- Returns:
A sparse matrix of random integers from a multinomial density for each row.
- Note:
It will works only if
phave csr format.
- grad(inputs, outputs_gradients)[source]#
Construct a graph for the gradient with respect to each input variable.
Each returned
Variablerepresents the gradient with respect to that input computed based on the symbolic gradients with respect to each output. If the output is not differentiable with respect to an input, then this method should return an instance of typeNullTypefor that input.Using the reverse-mode AD characterization given in [1]_, for a
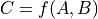 representing the function implemented by the
representing the function implemented by the Opand its two arguments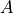 and
and 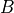 , given by the
, given by the
Variables ininputs, the values returned byOp.gradrepresent the quantities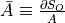 and
and
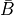 , for some scalar output term
, for some scalar output term 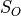 of
of 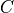 in
in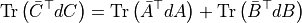
- Parameters:
inputs – The input variables.
output_grads – The gradients of the output variables.
- Returns:
grads – The gradients with respect to each
Variableininputs... [1] Giles, Mike. 2008. “An Extended Collection of Matrix Derivative Results for Forward and Reverse Mode Automatic Differentiation.”
- make_node(n, p)[source]#
Construct an
Applynode that represent the application of this operation to the given inputs.This must be implemented by sub-classes.
- Returns:
node – The constructed
Applynode.- Return type:
- perform(node, inputs, outputs)[source]#
Calculate the function on the inputs and put the variables in the output storage.
- Parameters:
node – The symbolic
Applynode that represents this computation.inputs – Immutable sequence of non-symbolic/numeric inputs. These are the values of each
Variableinnode.inputs.output_storage – List of mutable single-element lists (do not change the length of these lists). Each sub-list corresponds to value of each
Variableinnode.outputs. The primary purpose of this method is to set the values of these sub-lists.params – A tuple containing the values of each entry in
Op.__props__.
Notes
The
output_storagelist might contain data. If an element of output_storage is notNone, it has to be of the right type, for instance, for aTensorVariable, it has to be a NumPyndarraywith the right number of dimensions and the correct dtype. Its shape and stride pattern can be arbitrary. It is not guaranteed that such pre-set values were produced by a previous call to thisOp.perform(); they could’ve been allocated by anotherOp’sperformmethod. AnOpis free to reuseoutput_storageas it sees fit, or to discard it and allocate new memory.
- class aesara.sparse.sandbox.sp2.Poisson[source]#
Return a sparse having random values from a Poisson density with mean from the input.
WARNING: This Op is NOT deterministic, as calling it twice with the same inputs will NOT give the same result. This is a violation of Aesara’s contract for Ops
- Parameters:
x – Sparse matrix.
- Returns:
A sparse matrix of random integers of a Poisson density with mean of
xelement wise.
- grad(inputs, outputs_gradients)[source]#
Construct a graph for the gradient with respect to each input variable.
Each returned
Variablerepresents the gradient with respect to that input computed based on the symbolic gradients with respect to each output. If the output is not differentiable with respect to an input, then this method should return an instance of typeNullTypefor that input.Using the reverse-mode AD characterization given in [1]_, for a
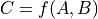 representing the function implemented by the
representing the function implemented by the Opand its two arguments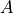 and
and 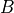 , given by the
, given by the
Variables ininputs, the values returned byOp.gradrepresent the quantities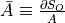 and
and
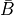 , for some scalar output term
, for some scalar output term 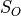 of
of 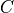 in
in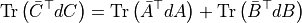
- Parameters:
inputs – The input variables.
output_grads – The gradients of the output variables.
- Returns:
grads – The gradients with respect to each
Variableininputs... [1] Giles, Mike. 2008. “An Extended Collection of Matrix Derivative Results for Forward and Reverse Mode Automatic Differentiation.”
- make_node(x)[source]#
Construct an
Applynode that represent the application of this operation to the given inputs.This must be implemented by sub-classes.
- Returns:
node – The constructed
Applynode.- Return type:
- perform(node, inputs, outputs)[source]#
Calculate the function on the inputs and put the variables in the output storage.
- Parameters:
node – The symbolic
Applynode that represents this computation.inputs – Immutable sequence of non-symbolic/numeric inputs. These are the values of each
Variableinnode.inputs.output_storage – List of mutable single-element lists (do not change the length of these lists). Each sub-list corresponds to value of each
Variableinnode.outputs. The primary purpose of this method is to set the values of these sub-lists.params – A tuple containing the values of each entry in
Op.__props__.
Notes
The
output_storagelist might contain data. If an element of output_storage is notNone, it has to be of the right type, for instance, for aTensorVariable, it has to be a NumPyndarraywith the right number of dimensions and the correct dtype. Its shape and stride pattern can be arbitrary. It is not guaranteed that such pre-set values were produced by a previous call to thisOp.perform(); they could’ve been allocated by anotherOp’sperformmethod. AnOpis free to reuseoutput_storageas it sees fit, or to discard it and allocate new memory.
