Shapes#
How Shape Information is Handled by Aesara#
Currently, information regarding shape is used in the following ways by Aesara:
To remove computations in the graph when we only want to know the shape, but not the actual value of a variable. This is done with the
Op.infer_shape()method.To generate faster compiled code (e.g. for a 2D convolution).
Example:
>>> import aesara
>>> x = aesara.tensor.matrix('x')
>>> f = aesara.function([x], (x ** 2).shape)
>>> aesara.dprint(f)
MakeVector{dtype='int64'} [id A] '' 2
|Shape_i{0} [id B] '' 1
| |x [id C]
|Shape_i{1} [id D] '' 0
|x [id C]
The output of this compiled function does not contain any multiplication or power computations; Aesara has removed them to compute the shape of the output directly.
Aesara propagates information about shapes within a graph using specialized
Ops and static Type information (see Types).
Specifying Exact Shape#
You can create variables with static shape information as follows:
aesara.tensor.tensor("float64", shape=(4, 3, 2))
You can also pass shape infomation directly to some Ops, like RandomVariables
aesara.tensor.random.normal(size=(7, 3, 5, 5))
You can use the
SpecifyShapeOpto add shape information anywhere in the graph. This allows to perform some optimizations. In the following example, this makes it possible to precompute the Aesara function to a constant.
>>> import aesara
>>> x = aesara.tensor.matrix()
>>> x_specify_shape = aesara.tensor.specify_shape(x, (2, 2))
>>> f = aesara.function([x], (x_specify_shape ** 2).shape)
>>> aesara.printing.debugprint(f)
DeepCopyOp [id A] '' 0
|TensorConstant{(2,) of 2} [id B]
Problems with Shape inference#
Sometimes this can lead to errors. Consider this example:
>>> import numpy as np
>>> import aesara
>>> x = aesara.tensor.matrix('x')
>>> y = aesara.tensor.matrix('y')
>>> z = aesara.tensor.join(0, x, y)
>>> xv = np.random.random((5, 4))
>>> yv = np.random.random((3, 3))
>>> f = aesara.function([x, y], z.shape)
>>> aesara.printing.debugprint(f)
MakeVector{dtype='int64'} [id A] '' 4
|Elemwise{Add}[(0, 0)] [id B] '' 3
| |Shape_i{0} [id C] '' 2
| | |x [id D]
| |Shape_i{0} [id E] '' 1
| |y [id F]
|Shape_i{1} [id G] '' 0
|x [id D]
>>> f(xv, yv) # DOES NOT RAISE AN ERROR AS SHOULD BE.
array([8, 4])
>>> f = aesara.function([x,y], z)# Do not take the shape.
>>> aesara.printing.debugprint(f)
Join [id A] '' 0
|TensorConstant{0} [id B]
|x [id C]
|y [id D]
>>> f(xv, yv)
Traceback (most recent call last):
...
ValueError: ...
As you can see, when asking only for the shape of some computation (join in the
example above), an inferred shape is computed directly, without executing
the computation itself (there is no join in the first output or debugprint).
This makes the computation of the shape faster, but it can also hide errors. In
this example, the computation of the shape of the output of join is done only
based on the first input Aesara variable, which leads to an error.
This might happen with other Ops such as Elemwise and Dot, for example.
Indeed, to perform some optimizations/rewrites (for speed or stability, for instance),
Aesara assumes that the computation is correct and consistent
in the first place, as it does here.
You can detect those problems by running the code without this optimization,
using the Aesara flag optimizer_excluding=local_shape_to_shape_i. You can
also obtain the same effect by running in the modes FAST_COMPILE or
DebugMode.
Broadcasting#
Broadcasting is a mechanism which allows tensors with different numbers of dimensions to be added or multiplied together by (virtually) replicating the smaller tensor along the dimensions that it is lacking.
Broadcasting is the mechanism by which a scalar may be added to a matrix, a vector to a matrix or a scalar to a vector.
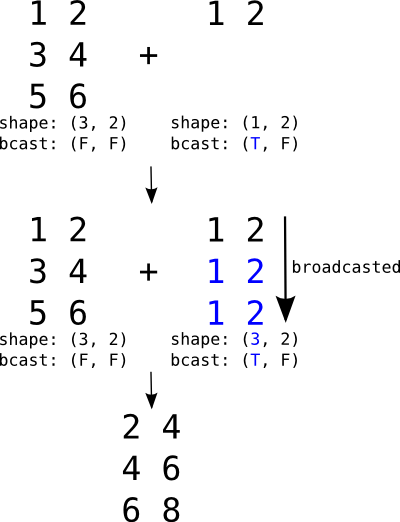
Broadcasting a row matrix. T and F respectively stand for True and False and indicate along which dimensions we allow broadcasting.
If the second argument were a vector, its shape would be
(2,) and its broadcastable pattern (False,). They would
be automatically expanded to the left to match the
dimensions of the matrix (adding 1 to the shape and True
to the pattern), resulting in (1, 2) and (True, False).
It would then behave just like the example above.
Unlike numpy which does broadcasting dynamically, Aesara needs to know, for any operation which supports broadcasting, which dimensions will need to be broadcasted. When applicable, this information is given in the Type of a Variable.
The following code illustrates how rows and columns are broadcasted in order to perform an addition operation with a matrix:
>>> r = at.row()
>>> r.broadcastable
(True, False)
>>> mtr = at.matrix()
>>> mtr.broadcastable
(False, False)
>>> f_row = aesara.function([r, mtr], [r + mtr])
>>> R = np.arange(3).reshape(1, 3)
>>> R
array([[0, 1, 2]])
>>> M = np.arange(9).reshape(3, 3)
>>> M
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
>>> f_row(R, M)
[array([[ 0., 2., 4.],
[ 3., 5., 7.],
[ 6., 8., 10.]])]
>>> c = at.col()
>>> c.broadcastable
(False, True)
>>> f_col = aesara.function([c, mtr], [c + mtr])
>>> C = np.arange(3).reshape(3, 1)
>>> C
array([[0],
[1],
[2]])
>>> M = np.arange(9).reshape(3, 3)
>>> f_col(C, M)
[array([[ 0., 1., 2.],
[ 4., 5., 6.],
[ 8., 9., 10.]])]
In these examples, we can see that both the row vector and the column vector are broadcasted in order to be be added to the matrix.
See the Numpy documentation for an in-depth explanation of the broadcasting mechanism.
