aesara.tensor.cov#
- aesara.tensor.cov(m, y=None, rowvar=True, bias=False, ddof=None, fweights=None, aweights=None)[source]#
Calculate the covariance matrix.
Covariance indicates the level to which two variables vary together. If we examine N-dimensional samples,
![m = [x_1, x_2, ... x_N]^T](../../../_images/math/7b63ef51161cb94c793b4eb2da96508ddf2d7ba5.png) ,
then the covariance matrix element
,
then the covariance matrix element 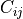 is the covariance of
is the covariance of
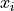 and
and 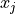 . The element
. The element 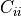 is the variance
of
is the variance
of 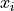 . Code and docstring ported from numpy.
. Code and docstring ported from numpy.- Parameters:
m (array_like) – A 2-D array containing multiple variables and observations. Each row of
mrepresents a variable, and each column is observations of all those variables.y (array_like, optional) – An additional set of variables and observations.
yhas the same form as that ofm.rowvar (bool, optional) – If
rowvaris True (default), then each row represents a variable, with observations in the columns. Otherwise, the relationship is transposed: each column represents a variable, while the rows contain observations.bias (bool, optional) – Default normalization (False) is by
(N - 1), whereNis the number of observations given (unbiased estimate). Ifbiasis True, then normalization is byN. These values can be overridden by using the keywordddof.ddof (int, optional) – If not
Nonethe default value implied bybiasis overridden. The default value isNone.
- Returns:
out
- Return type:
The covariance matrix of the variables.
